题目内容
数列{an}中,a1= ,前n项的和Sn=n2an,则an+1=________.
,前n项的和Sn=n2an,则an+1=________.
 ,前n项的和Sn=n2an,则an+1=________.
,前n项的和Sn=n2an,则an+1=________.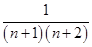
an=Sn-Sn-1=n2an-(n-1)2an-1(n≥2),
∴(n2-1)an=(n-1)2an-1(n≥2),
故=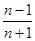 (n≥2),
(n≥2),
∴an=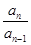 ·
·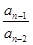 ·…·
·…·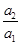 ·a1
·a1
=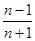 ·
·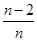 ·…·
·…·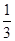 ·
·
=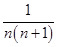 (n≥2),
(n≥2),
当n=1时,也符合,
∴an+1=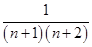 .
.
∴(n2-1)an=(n-1)2an-1(n≥2),
故=
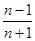 (n≥2),
(n≥2),∴an=
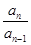 ·
·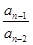 ·…·
·…·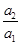 ·a1
·a1=
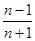 ·
·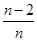 ·…·
·…·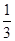 ·
·
=
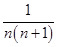 (n≥2),
(n≥2),当n=1时,也符合,
∴an+1=
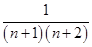 .
.
练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的前n项和为
的前n项和为 ,公差
,公差
 成等比数列
成等比数列 的通项公式;
的通项公式; 中依次取出第2项、第4项、第8项,
中依次取出第2项、第4项、第8项, ,按原来顺序组成一个新数列
,按原来顺序组成一个新数列 ,且这个数列的前
,且这个数列的前 的表达式.
的表达式.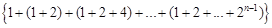 的前
的前 项和为_____________.
项和为_____________. ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( ) 的通项公式是
的通项公式是 ,
, ( )
( )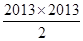

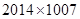

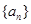 的前n项和为
的前n项和为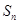 ,若
,若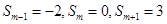 ,则
,则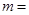 ( )
( ) ,2
,2  ,3
,3  ,4
,4  ,…的前n项和为 .
,…的前n项和为 .