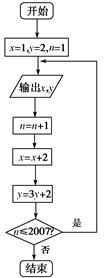
题目内容
已知函数f(n)= ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
 ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )| A.-2013 | B.-2014 | C.2013 | D.2014 |
D
当n为奇数时,an=f(n)+f(n+1)=n2-(n+1)2=-(2n+1);当n为偶数时,an=f(n)+f(n+1)=-n2+(n+1)2=2n+1.所以a1+a2+a3+…+a2014=2(-1+2-3+4+…-2013+2014)=2014.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 ,求证:
,求证: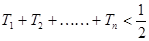 .
.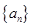 的前
的前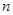 项和为
项和为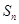 ,且
,且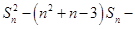
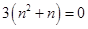 ,
,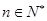 .
.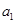 的值;
的值;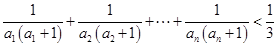 .
. 前
前 项和
项和 .
. ,前n项的和Sn=n2an,则an+1=________.
,前n项的和Sn=n2an,则an+1=________.