题目内容

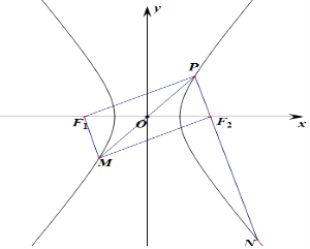
【题目】已知双曲线C： ﹣ =1（a＞0，b＞0）的左、右焦点分别为F1 ， F2 ， O为坐标原点，点P是双曲线在第一象限内的点，直线PO，PF2分别交双曲线C的左、右支于另一点M，N，若|PF1|=2|PF2|，且∠MF2N=120°，则双曲线的离心率为（ ）
A.
B.
C.
D.

【答案】B
【解析】解：由题意，|PF1|=2|PF2|，

由双曲线的定义可得，|PF1|﹣|PF2|=2a，

可得|PF1|=4a，|PF2|=2a

由四边形PF1MF2为平行四边形，

又∠MF2N=120°，可得∠F1PF2=120°，

在三角形PF1F2中，由余弦定理可得

4c2=16a2+4a2﹣24a2acos120°，

即有4c2=20a2+8a2，即c2=7a2，

可得c= a，

即e= = ．

故选B．

练习册系列答案
相关题目

【题目】抛物线C：y2=4x的焦点为F，准线为l，P为抛物线C上一点，且P在第一象限，PM⊥l于点M，线段MF与抛物线C交于点N，若PF的斜率为 ，则 =（ ）
A.
B.
C.
D.

【题目】若a＞b＞1，0＜c＜1，则（ ）
A.ac＜bc
B.abc＜bac
C.alogbc＜blogac
D.logac＜logbc

【题目】若函数f（x）= +ln（ +x）+ cos xdx在区间[﹣k，k]（k＞0）上的值域为[m，n]，则m+n的值是（ ）
A.0
B.2
C.4
D.6

【题目】在如图所示的直三棱柱ABC﹣A1B1C1中，面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直，D为AA1的中点，E为BC1的中点．
（Ⅰ）证明：DE∥平面A1B1C1；
（Ⅱ）求平面C1BD和平面CBD所成的角（锐角）的余弦值．

【题目】如图，在三棱柱ABC﹣A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1﹣BC1﹣B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求 的值．

【题目】如图，四棱锥P﹣ABCD中，底面ABCD为平行四边形，∠DAB=60°，AB=2AD，PD⊥底面ABCD．
（Ⅰ）证明：PA⊥BD；
（Ⅱ）若PD=AD，求二面角A﹣PB﹣C的余弦值．

【题目】已知数列{an}满足a1=3，an+1=2an﹣n+1，数列{bn}满足b1=2，bn+1=bn+an﹣n．
（1）证明：{an﹣n}为等比数列；
（2）数列{cn}满足 ，求数列{cn}的前n项和Tn ， 求证：Tn ．

【题目】根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2.5的年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米．我市环保局随机抽取了一居民区2016年20天PM2.5的24小时平均浓度（单位：微克/立方米）的监测数据，数据统计如表：

组别

PM2.5浓度（微克/立方米）

频数（天）

频率

第一组

（0，25]

3

0.15

第二组

（25，50]

12

0.6

第三组

（50，75]

3

0.15

第四组

（75，100]

2

0.1


（1）将这20天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图． ①求频率分布直方图中a的值；
②求样本平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由．
（2）将频率视为概率，对于2016年的某3天，记这3天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为X，求X的分布列．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网