题目内容
【题目】若函数f(x)= ![]() +ln(
+ln( ![]() +x)+
+x)+ ![]() cos xdx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n的值是( )
cos xdx在区间[﹣k,k](k>0)上的值域为[m,n],则m+n的值是( )
A.0
B.2
C.4
D.6
【答案】B
【解析】解:f(x)= ![]() +ln(
+ln( ![]() +x)+
+x)+ ![]() cos xdx
cos xdx
= ![]() +ln(
+ln( ![]() +x)+
+x)+ ![]()
= ![]() +ln(
+ln( ![]() +x)+sinx
+x)+sinx
= ![]() .
.
令g(x)= ![]() ,定义域为R,
,定义域为R,
又g(﹣x)= ![]()
= 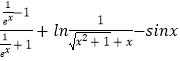
=﹣ ![]()
=﹣g(x).
∴g(x)为奇函数,
∵f(x)=g(x)+1,
∴g(x)=f(x)﹣1,
∵f(x)在区间[﹣k,k](k>0)上的值域为[m,n],
∴当f(x)取得最大值n时,g(x)也取得最大值g(x)max=n﹣1,
f(x)取得最小值m时,g(x)也取得最小值g(x)min=m﹣1,
∵函数g(x)的图象关于原点对称,
∴函数g(x)在区间[﹣k,k](k>0)上的最大值和最小值互为相反数,
即g(x)max+g(x)min=n﹣1+m﹣1=0,
∴m+n=2.
故选:B.
【考点精析】根据题目的已知条件,利用函数的值域的相关知识可以得到问题的答案,需要掌握求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.