题目内容
【题目】在如图所示的直三棱柱ABC﹣A1B1C1中,面AA1B1B和面AA1C1C都是边长为1的正方形且互相垂直,D为AA1的中点,E为BC1的中点. 
(Ⅰ)证明:DE∥平面A1B1C1;
(Ⅱ)求平面C1BD和平面CBD所成的角(锐角)的余弦值.
【答案】解:(Ⅰ)证明:如图,过E作EF∥BC交BC于F,
∵E为BC1的中点,∴EF为△BB1C1的中位线,则EF= ![]() ,
,
又D为AA1中点,∴D ![]() ,
,
∵四边形AA1B1B为正方形,∴EF∥DA1,且EF=DA1,
∴四边形DA1FE为平行四边形,则DE∥A1F,
∵DE平面A1B1C1,A1F平面A1B1C1,
∴DE∥平面A1B1C1;
(Ⅱ)解:∵AA1C1C是正方形,∴AC⊥AA1,
又平面AA1B1B⊥平面AA1C1C,且平面AA1B1B⊥平面AA1C1C,
∴AC⊥平面AA1B1B,则AC⊥BC.
分别以BA、AD、AC所在直线为x、y、z轴建立空间直角坐标系,
则C(0,0,1),D(0, ![]() ,0),B(﹣1,0,0),C1(0,1,1),
,0),B(﹣1,0,0),C1(0,1,1),
![]() ,
, ![]() ,
, ![]() .
.
设平面BCD的一个法向量为 ![]() ,
,
由 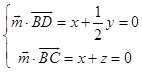 ,令y=2,得
,令y=2,得 ![]() ;
;
设平面C1BD的一个法向量为 ![]() ,
,
由 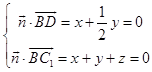 ,令y=2,得
,令y=2,得 ![]() .
.
∴cos< ![]() >=
>= ![]() .
.
∴平面C1BD和平面CBD所成的角(锐角)的余弦值为 ![]() .
.
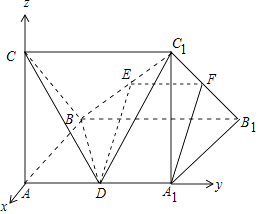
【解析】(Ⅰ)过E作EF∥BC交BC于F,可得EF为△BB1C1的中位线,结合已知可得EF∥DA1,且EF=DA1,则四边形DA1FE为平行四边形,得DE∥A1F,由线面平行的判定可得DE∥平面A1B1C1;(Ⅱ)由题意可得AC⊥平面AA1B1B,则AC⊥BC.分别以BA、AD、AC所在直线为x、y、z轴建立空间直角坐标系,求出所用点的坐标,得到平面C1BD和平面CBD的一个法向量,由两法向量所成角的余弦值可得平面C1BD和平面CBD所成的角(锐角)的余弦值.
【考点精析】掌握直线与平面平行的判定是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】某省高考改革新方案,不分文理科,高考成绩实行“3+3”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S,从学生群体S中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 5 | 25 | 20 |
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X的分布列和数学期望;
(III)将频率视为概率,现从学生群体S中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y,求事件“y≥2”的概率.
【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.

