Question

【题目】如图，在三棱柱ABC﹣A1B1C1中，AA1C1C是边长为4的正方形．平面ABC⊥平面AA1C1C，AB=3，BC=5．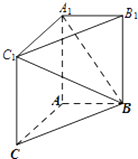
（Ⅰ）求证：AA1⊥平面ABC；
（Ⅱ）求证二面角A1﹣BC1﹣B1的余弦值；
（Ⅲ）证明：在线段BC1上存在点D，使得AD⊥A1B，并求 的值．

Answer 1

【答案】解：（I）证明：∵AA1C1C是正方形，∴AA1⊥AC．

又∵平面ABC⊥平面AA1C1C，平面ABC∩平面AA1C1C=AC，

∴AA1⊥平面ABC．

（II）解：由AC=4，BC=5，AB=3．

∴AC2+AB2=BC2，∴AB⊥AC．

建立如图所示的空间直角坐标系，则A1（0，0，4），B（0，3，0），B1（0，3，4），C1（4，0，4），

∴ ， ， ．

设平面A1BC1的法向量为 ，平面B1BC1的法向量为 =（x2，y2，z2）．

则 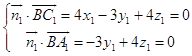，令y1=4，解得x1=0，z1=3，∴ ．

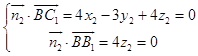，令x2=3，解得y2=4，z2=0，∴ ．

= = = ．

∴二面角A1﹣BC1﹣B1的余弦值为 ．

（III）设点D的竖坐标为t，（0＜t＜4），在平面BCC1B1中作DE⊥BC于E，可得D ，

∴ = ， =（0，3，﹣4），

∵ ，∴ ，

∴ ，解得t= ．

∴ ．

【解析】（I）利用AA1C1C是正方形，可得AA1⊥AC，再利用面面垂直的性质即可证明（II）利用勾股定理的逆定理可得AB⊥AC．通过建立空间直角坐标系，利用两个平面的法向量的夹角即可得到二面角；（III）设点D的竖坐标为t，（0＜t＜4），在平面BCC1B1中作DE⊥BC于E，可得D ，利用向量垂直于数量积得关系即可得出．
【考点精析】通过灵活运用直线与平面垂直的判定，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想即可以解答此题．