题目内容
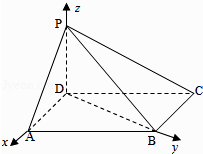
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD. 
(Ⅰ)证明:PA⊥BD;
(Ⅱ)若PD=AD,求二面角A﹣PB﹣C的余弦值.
【答案】解:(Ⅰ)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD= ![]() ,
,
从而BD2+AD2=AB2,故BD⊥AD
又PD⊥底面ABCD,可得BD⊥PD
所以BD⊥平面PAD.故PA⊥BD
(Ⅱ)如图,以D为坐标原点,AD的长为单位长,
射线DA为x轴的正半轴建立空间直角坐标系D﹣xyz,则
A(1,0,0),B(0, ![]() ,0),C(﹣1,
,0),C(﹣1, ![]() ,0),P(0,0,1).
,0),P(0,0,1).
![]() =(﹣1,
=(﹣1, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,﹣1),
,﹣1), ![]() =(﹣1,0,0),
=(﹣1,0,0),
设平面PAB的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 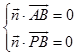
即  ,
,
因此可取 ![]() =(
=( ![]() ,1,
,1, ![]() )
)
设平面PBC的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 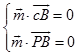 ,
,
即: 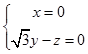
可取 ![]() =(0,1,
=(0,1, ![]() ),cos<
),cos< ![]() >=
>= ![]() =
= ![]()
故二面角A﹣PB﹣C的余弦值为:﹣ ![]() .
.
【解析】(Ⅰ)因为∠DAB=60°,AB=2AD,由余弦定理得BD= ![]() ,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;(Ⅱ)建立空间直角坐标系,写出点A,B,C,P的坐标,求出向量
,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;(Ⅱ)建立空间直角坐标系,写出点A,B,C,P的坐标,求出向量 ![]() ,和平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可.
,和平面PAB的法向量,平面PBC的法向量,求出这两个向量的夹角的余弦值即可.
【考点精析】认真审题,首先需要了解直线与平面垂直的性质(垂直于同一个平面的两条直线平行).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(Ⅰ)求一续保人本年度的保费高于基本保费的概率;
(Ⅱ)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(Ⅲ)求续保人本年度的平均保费与基本保费的比值.

