题目内容
【题目】已知从圆C：（x+1）2+（y﹣2）2=2外一点P（x1 ， y1）向该圆引一条切线，切点为M，O为坐标原点，且有|PM|=|PO|，则当|PM|取最小值时点P的坐标为 ．
【答案】（﹣ 
， 
）
【解析】解：如图所示，⊙C：x2+y2+2x﹣4y+3=0化为（x+1）2+（y﹣2）2=2，圆心C（﹣1，2），半径r= 
． 因为|PM|=|PO|，
所以|PO|2+r2=|PC|2（C为圆心，r为圆的半径），
所以x12+y12+2=（x1+1）2+（y1﹣2）2 ， 即2x1﹣4y1+3=0．要使|PM|最小，只要|PO|最小即可．
当直线PO垂直于直线2x﹣4y+3=0时，即直线PO的方程为2x+y=0时，|PM|最小，此时P点即为两直线的交点，得P点坐标（﹣ ， ）．
所以答案是（﹣ ， ）．
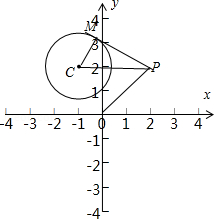
练习册系列答案
相关题目
