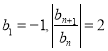Question

【题目】如图，四棱锥P﹣ABCD中，底面ABCD是直角梯形，∠DAB＝90°AD∥BC，AD⊥侧面PAB，△PAB是等边三角形，DA＝AB＝2，BC，E是线段AB的中点.

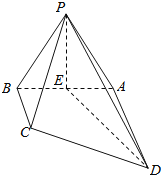
（1）求证：PE⊥CD；

（2）求PC与平面PDE所成角的正弦值.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）先证明，再证明，又，推出PE⊥平面ABCD，然后证明PE⊥CD；

（2）以E为原点，建立如图所示的空间直角坐标系，推出（2，1，0），（0，0，），（1，﹣1，），设（x，y，z）为平面PDE的一个法向量，由 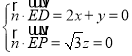可以求得（1，﹣2，0），设PC与平面PDE所成的角为θ，利用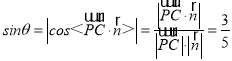，最后得出PC与平面PDE所成角的正弦值为.

（1）∵AD⊥侧面PAB，PE平面PAB，∴AD⊥EP.

又∵△PAB是等边三角形，E是线段AB的中点，∴AB⊥EP.

∵AD∩AB＝A，∴PE⊥平面ABCD.

∵CD平面ABCD，∴PE⊥CD.

（2）以E为原点，EA、EP分别为y、z轴，建立如图所示的空间直角坐标系.

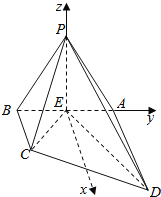
则E（0，0，0），C（1，﹣1，0），D（2，1，0），P（0，0，）.

（2，1，0），（0，0，），（1，﹣1，）.

设（x，y，z）为平面PDE的一个法向量.

由 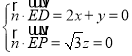，令x＝1，可得（1，﹣2，0）

设PC与平面PDE所成的角为θ，得

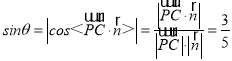
所以PC与平面PDE所成角的正弦值为.