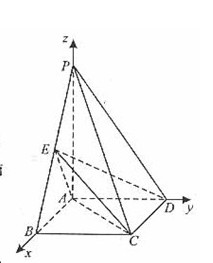
题目内容
本小题满分12分)
已知斜三棱柱ABC—A1B1C1,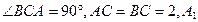 在底面ABC上的射影恰为AC的中点D,又知
在底面ABC上的射影恰为AC的中点D,又知 w.& (I)求证:AC1⊥平面A1BC;
w.& (I)求证:AC1⊥平面A1BC;
(II)求CC1到平面A1AB的距离;
(理)(III)求二面角A—A1B—C的大小
|
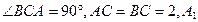 在底面ABC上的射影恰为AC的中点D,又知
在底面ABC上的射影恰为AC的中点D,又知 w.& (I)求证:AC1⊥平面A1BC;
w.& (I)求证:AC1⊥平面A1BC;(II)求CC1到平面A1AB的距离;
(理)(III)求二面角A—A1B—C的大小
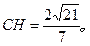 ,
,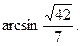
解:(I)因为A1D⊥平面ABC,
所以平面AA1C1C⊥平面ABC, …………1分
又BC⊥AC,所以BC⊥平面AA1C1C,
得BC⊥AC1,又BA1⊥AC1 w.&…………2分
所以AC1⊥平面A1BC; …………3分
(II)因为AC1⊥A1C,所以四边形AA1C1C为菱形,
故AA1=AC=2,又D为AC中点,知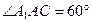 …………4分
…………4分
取AA1中点F,则AA1⊥平面BCF,从而平面A1AB⊥平面BCF,…………6分
过C作CH⊥BF于H,则CH⊥面A1AB,
在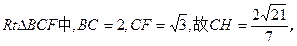 …………7分
…………7分
即CC1到平面A1AB的距离为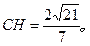 …………8分
…………8分
(III)过H作HG⊥A1B于G,连CG,则CG⊥A1B,
从而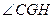 为二面角A—A1B—C的平面角, …………9分
为二面角A—A1B—C的平面角, …………9分
在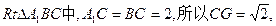
在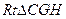 中,
中,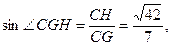 w.&…………11分
w.&…………11分
故二面角A—A1B—C的大小为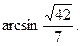 …………12分
…………12分
所以平面AA1C1C⊥平面ABC, …………1分
又BC⊥AC,所以BC⊥平面AA1C1C,
得BC⊥AC1,又BA1⊥AC1 w.&…………2分
所以AC1⊥平面A1BC; …………3分
(II)因为AC1⊥A1C,所以四边形AA1C1C为菱形,
故AA1=AC=2,又D为AC中点,知
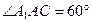 …………4分
…………4分取AA1中点F,则AA1⊥平面BCF,从而平面A1AB⊥平面BCF,…………6分
过C作CH⊥BF于H,则CH⊥面A1AB,
在
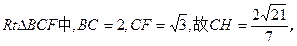 …………7分
…………7分即CC1到平面A1AB的距离为
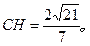 …………8分
…………8分(III)过H作HG⊥A1B于G,连CG,则CG⊥A1B,
从而
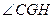 为二面角A—A1B—C的平面角, …………9分
为二面角A—A1B—C的平面角, …………9分在
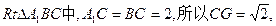
在
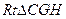 中,
中,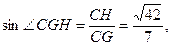 w.&…………11分
w.&…………11分故二面角A—A1B—C的大小为
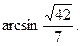 …………12分
…………12分
练习册系列答案
相关题目

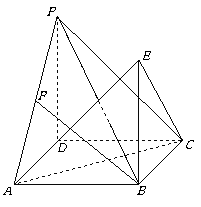
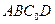 中,
中,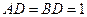 ,
,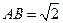 。沿它的对角线
。沿它的对角线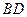 把△
把△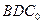 折起,使点
折起,使点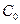 到达平面
到达平面 的位置。
的位置。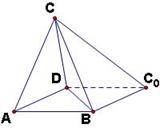
 平面
平面 ;
;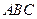 为等腰三角形,求二面角
为等腰三角形,求二面角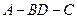 的大小。
的大小。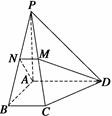
 平面ABCD、M、N、E分别是AB、PC、CD的中点。
平面ABCD、M、N、E分别是AB、PC、CD的中点。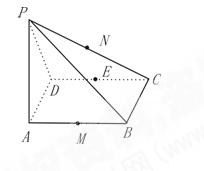
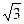 求二面角B-DC-A的正弦值。
求二面角B-DC-A的正弦值。 的球与正三棱柱的各个面都相切,则球与正三棱柱的体积比是( )
的球与正三棱柱的各个面都相切,则球与正三棱柱的体积比是( )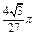
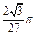
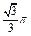
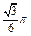
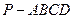 中,底面
中,底面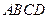 为矩形,
为矩形,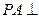 底面
底面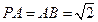 ,点
,点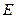 是棱
是棱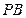 的中点.
的中点.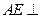 平面
平面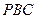 ;
;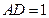 ,求二面角
,求二面角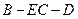 的平面角的余弦值.
的平面角的余弦值.