题目内容
3.某数学老师身高175cm,他爷爷、父亲和儿子的身高分别是172cm、169cm、和181cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为184cm.分析 利用最小二乘法求回归系数,得回归直线方程,代入儿子的身高可得即可预测变量孙子的身高.
解答 解:根据题意可得:
| 父亲的身高x(cm) | 172 | 169 | 175 |
| 儿子的身高y(cm) | 169 | 175 | 181 |
$\overline{y}$=$\frac{169+175+181}{3}$=175,
直接计算得:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{18}{18}$=1,
$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=175-1×172=3,
∴预测该教师孙子的身高y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$=1×181+3=184cm,
故答案为:184.
点评 本题考查线性回归方程,列出表格是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
8.已知tanα=2,则$\frac{1+2sinαcosα}{{{{sin}^2}α-{{cos}^2}α}}$的值是( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | -$\frac{1}{3}$ | D. | -3 |
13.函数f(x)=$\sqrt{{x^2}+2x-3}$的递增区间为( )
| A. | [-1,+∞) | B. | [1,+∞) | C. | [-3,1] | D. | (-∞,-1] |
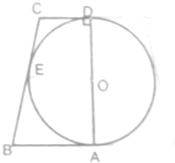 如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比.
如图,半圆O的直径为直角梯形垂直于底的腰,且切AB、BC、CD于A、E、D点,将其绕AD所在直线旋转一周,得到一个球与一个圆台,若球的表面积与圆台侧面积的比为3:4,求球的体积与圆台体积之比.