题目内容
11．
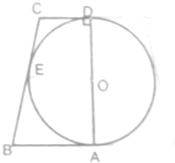如图，半圆O的直径为直角梯形垂直于底的腰，且切AB、BC、CD于A、E、D点，将其绕AD所在直线旋转一周，得到一个球与一个圆台，若球的表面积与圆台侧面积的比为3：4，求球的体积与圆台体积之比．
分析 设球半径为R，圆台上底半径为r，圆台下底半径为r′，因为球与圆台上下侧面都相切，所以圆台侧面长l=r+r′，结合已知求出r，r′，R之间的关系式，代入球的体积公式和圆台的体积公式，可得答案．
解答 解：设球半径为R，圆台上底半径为r，圆台下底半径为r′，
因为球与圆台上下侧面都相切，所以圆台侧面长l=r+r′，
又∵球面面积与圆台的侧面积之比为3：4，
∴π﹙r+r′﹚2：4πR2=4：3①
﹙r′-r﹚2+﹙2R﹚2=﹙r+r′﹚2②
解之r′=3r，则R=$\sqrt{3}$r，
V球=$\frac{4}{3}$πR3=$\frac{12\sqrt{3}π}{3}$r3，
V台=$\frac{1}{3}$π（r2+r′2+rr′）2R=$\frac{26\sqrt{3}π}{3}$r3，
V球：V台=6：13．
点评 本题考查的知识点是旋转体，熟练掌握圆台和球的表面积公式和体积公式，是解答的关键．
练习册系列答案
口算题天天练系列答案
相关题目
1．已知集合A={x|$\frac{x-1}{x+2}$≥0}，B={x|x≤a}，若A∩B=B，则a的取值范围是（ ）
| A． | a≥1 | B． | a≥2 | C． | a≤-2 | D． | a＜-2 |
19．已知正项等比数列{an}满足：a7=a6+2a5，若存在两项am、an，使得aman=16a12，则$\frac{1}{m}$+$\frac{9}{n}$的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{8}{3}$ | C． | $\frac{11}{4}$ | D． | 不存在 |
6．已知集合A={x|1≤x≤3}，B={-1，1，2，3}，则A∩B等于（ ）
| A． | {1，2} | B． | {2，3} | C． | {1，2，3} | D． | {-1，1，2，3} |