题目内容
13.已知A,B,C三点在同一球面上,若球心到平面ABC的距离为1,AB=1,AC=2,∠BAC=60°,则球的体积为$\frac{8\sqrt{2}}{3}π$.分析 由“∠BAC=60°,AB=1,AC=2,”得到AB即为A、B、C三点所在圆的直径,取AB的中点M,连接OM,则OM即为球心到平面ABC的距离,在Rt△OMB中,OM=1,MB=1,则OB可求,从而得出该球的体积.
解答  解:在三角形ABC中,∠BAC=60°,AB=1,AC=2,∴BC=$\sqrt{3}$,
解:在三角形ABC中,∠BAC=60°,AB=1,AC=2,∴BC=$\sqrt{3}$,
则三角形ABC是以AC为斜边的直角三角形,
如图所示:
取AC的中点M,则球面上A、B、C三点所在的圆即为⊙M,连接OM,则OM即为球心到平面ABC的距离,
在Rt△OMB中,OM=1,MA=1,
∴OA=$\sqrt{2}$,即球球的半径为$\sqrt{2}$.
∴球的体积为:$\frac{4}{3}π×(\sqrt{2})^{3}$=$\frac{8\sqrt{2}}{3}π$.
故答案为:$\frac{8\sqrt{2}}{3}π$.
点评 本题考查球的有关计算问题,点到平面的距离,是基础题.

练习册系列答案
相关题目
3.如图所示的程序框图,若输出结果是990,则判断框内应填入的条件是( )
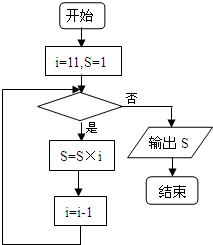

| A. | i≥10 | B. | i<10 | C. | i≥9 | D. | i<9 |
4.极坐标方程ρ=2$\sqrt{2}$cos($\frac{π}{4}$-θ)表示图形的面积是( )
| A. | 2 | B. | 2π | C. | 4 | D. | 4π |
1.已知集合A={x|$\frac{x-1}{x+2}$≥0},B={x|x≤a},若A∩B=B,则a的取值范围是( )
| A. | a≥1 | B. | a≥2 | C. | a≤-2 | D. | a<-2 |
8.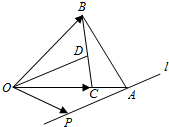 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
 在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )
在△OAB中,C为OA上的一点,且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$,D是BC的中点,过点A的直线l∥OD,P是直线l上的动点,若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$,则λ1-λ2=( )| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | $\frac{5}{4}$ | D. | -$\frac{5}{4}$ |
18.一船向正北方向航行,看见它的正西方向有相距10海里的两个灯塔恰好与它在一条直线上.船继续航行半小时后,看见这两个灯塔恰好与它在一条直线上.船继续航行半个小时后,看见这两个灯塔中,一灯塔在船的南偏西60°方向上,另一灯塔在船的南偏西75°方向上,则这艘船的速度是每小时( )
| A. | 5$\sqrt{2}$海里 | B. | 5 海里 | C. | 10$\sqrt{2}$海里 | D. | 10海里 |