题目内容
18．将二进制数$\stackrel{10位}{\overbrace{（11…11）_{2}}}$转换成十进制形式是1023．分析 根据二进制数转化成十进制数的规则，二进制数第0位的权值是2的0次方，第1位的权值是2的1次方…，可转化为等比数列的和，利用等比数列的求和公式，即可得出结论．
解答 解：由题意，二进制数$\stackrel{10位}{\overbrace{（11…11）_{2}}}$=1×29+1×28+…+1×20=$\frac{1×（1-{2}^{10}）}{1-2}$=210-1=1023．
故答案为：1023．
点评 本题考查二进制数转化成十进制数，掌握规则是关键，属于基础题．
练习册系列答案
相关题目
8．
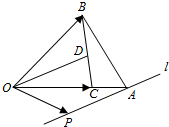在△OAB中，C为OA上的一点，且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$，则λ1-λ2=（ ）
在△OAB中，C为OA上的一点，且$\overrightarrow{OC}=\frac{4}{5}\overrightarrow{OA}$，D是BC的中点，过点A的直线l∥OD，P是直线l上的动点，若$\overrightarrow{OP}={λ_1}\overrightarrow{OB}+{λ_2}\overrightarrow{OC}$，则λ1-λ2=（ ）| A． | $\frac{3}{2}$ | B． | -$\frac{3}{2}$ | C． | $\frac{5}{4}$ | D． | -$\frac{5}{4}$ |
6．已知集合A={x|1≤x≤3}，B={-1，1，2，3}，则A∩B等于（ ）
| A． | {1，2} | B． | {2，3} | C． | {1，2，3} | D． | {-1，1，2，3} |
10．已知数列{an}的前n项和为Sn，若an=$\frac{1}{{\sqrt{n}+\sqrt{n+1}}}$，Sn=10，则n=（ ）
| A． | 90 | B． | 121 | C． | 119 | D． | 120 |
7．（1+i）20-（1-i）20的值为（ ）
| A． | 0 | B． | 1024 | C． | -1024 | D． | -10241 |