题目内容
【题目】在直角坐标系
中，圆
的参数方程为
为参数)，直线
经过点
，且倾斜角为
．
(1)写出直线的参数方程和圆的标准方程；
(2)设直线与圆相交于
两点，求
的值．
【答案】（1）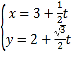
(t为参数)，
；（2）12.
【解析】
(1)根据参数方程与普通方程的互化可得到圆的直角坐标方程，由直线的参数方程的写法得到直线的参数方程；（2）；联立直线的参数方程和圆的普通方程，得到|PA|·|PB|＝|t1t2|可得到结果.
(1)把圆C的参数方程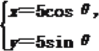
(θ为参数)化为直角坐标方程为x2＋y2＝25．
由条件可得直线l的参数方程为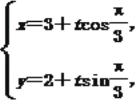
即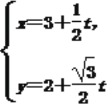
(t为参数)．
(2)把直线l的参数方程代入圆C的方程化简可得t2＋(3＋2
)t－12＝0，
所以t1t2＝－12，故|PA|·|PB|＝|t1t2|＝12．
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
附：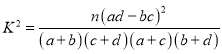
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
则下列说法正确的是（ ）
A.有
以上的把握认为“爱好该项运动与性别无关”
B.有
以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过
的前提下，认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过
的前提下，认为“爱好该项运动与性别有关”
【题目】某餐厅通过查阅了最近5次食品交易会参会人数
(万人)与餐厅所用原材料数量
(袋)，得到如下统计表：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
（1）根据所给5组数据，求出
关于
的线性回归方程
.
（2）已知购买原材料的费用
(元)与数量
(袋)的关系为
，
投入使用的每袋原材料相应的销售收入为700元，多余的原材料只能无偿返还，据悉本次交易大会大约有15万人参加，根据(1)中求出的线性回归方程，预测餐厅应购买多少袋原材料，才能获得最大利润，最大利润是多少？(注：利润
销售收入
原材料费用).
参考公式： 
， 
.
参考数据： 
， 
， 
.
