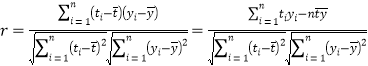Question

【题目】已知函数．

（1）求f[f（1）]的值；

（2）若f（x）＞1，求x的取值范围；

（3）判断函数在（-2，+∞）上的单调性，并用定义加以证明．

Answer 1

【答案】（1） （2）（-∞，-2） （3）增函数，证明见解析

【解析】

（1）可以求出，然后代入x=即可求出f[f（1）]的值；

（2）根据f（x）＞1即可得出，化简然后解分式不等式即可；

（3）分离常数得出，从而可看出f（x）在（-2，+∞）上是增函数，根据增函数的定义证明：设任意的x1＞x2＞-2，然后作差，通分，得出，然后说明f（x1）＞f（x2）即可得出f（x）在（-2，+∞）上是增函数．

（1）f[f（1）]=；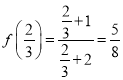

（2）由f（x）＞1得，，化简得，，

∴x＜-2，

∴x的取值范围为（-∞，-2）；

（3），f（x）在（-2，+∞）上是增函数，证明如下：

设x1＞x2＞-2，则：=，

∵x1＞x2＞-2，

∴x1-x2＞0，x1+2＞0，x2+2＞0，

∴，

∴f（x1）＞f（x2），

∴f（x）在（-2，+∞）上是增函数．