题目内容
已知数列{  }、{
}、{ 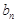 }满足:
}满足: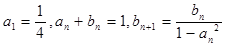 .
.
(1)求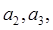
(2)证明:数列{ }为等差数列,并求数列
}为等差数列,并求数列 和{
和{ 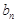 }的通项公式;
}的通项公式;
(3)设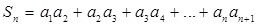 ,求实数
,求实数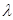 为何值时
为何值时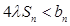 恒成立.
恒成立.
(1)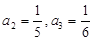 ;(2)
;(2)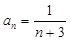 ,
,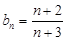 ;
;
解析试题分析:(1)由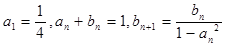 ,
,
可求出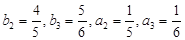 ;
;
(2)扣住等差数列的定义,从定义出发进行证明,
利用条件推导出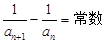 ,即得证:
,即得证:
∵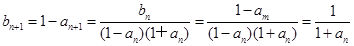
∴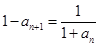 ,
,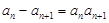
∴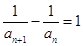
∴ 数列{ }是以4为首项,1为公差的等差数列
}是以4为首项,1为公差的等差数列
∴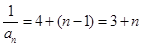
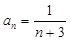 ∴
∴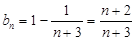
(3)借助前两问,利用裂项求和法,可得出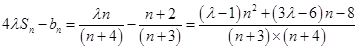 ,问题转化为
,问题转化为
设f(n)= 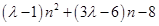 <0,恒成立问题,
<0,恒成立问题,
对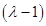 进行讨论,分三种情况,从而可得出答案,见详解.
进行讨论,分三种情况,从而可得出答案,见详解.
试题解析:(1) ∵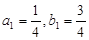 ∴
∴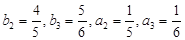
(2)∵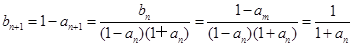
∴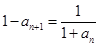 ,
,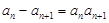
∴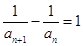 ,
,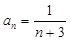 ∴
∴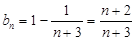
∴ 数列{ }是以4为首项,1为公差的等差数列
}是以4为首项,1为公差的等差数列
∴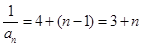
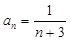 ∴
∴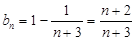
(3)已知 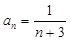 ,所以
,所以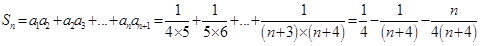
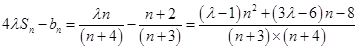
由条件可知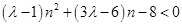 恒成立即可满足条件.
恒成立即可满足条件.
设f(n)= 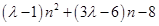
当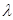 =1时,f(n)=-3n-8<0恒成立;
=1时,f(n)=-3n-8<0恒成立;
当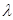 >1时,由二次函数的性质知不可能成立;
>1时,由二次函数的性质知不可能成立;
当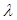 <1时,对称轴
<1时,对称轴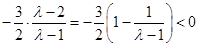 ,f(1)在
,f(1)在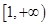 为单调递减函数,
为单调递减函数,
f(1)= 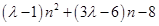 =
=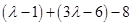 =4
=4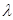 -15<0
-15<0
所以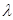 <
<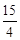
所以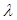 <1时
<1时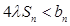 恒成立
恒成立
综上知,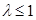 时 ,
时 ,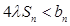 恒成立 .
恒成立 .
考点:等差数列,等比数列,二次函数,分类讨论.

练习册系列答案
相关题目
 的首项为
的首项为 、公差为2,则它的前n项
、公差为2,则它的前n项 的最小值是______________。
的最小值是______________。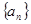 的前三项为
的前三项为 ,则此数列的通项公式为______ .
,则此数列的通项公式为______ .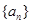 是等差数列,
是等差数列,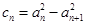 (
( ).
). 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;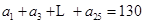 ,
, (
( 为常数),试写出数列
为常数),试写出数列 项和为
项和为 ,问是否存在这样的实数
,问是否存在这样的实数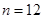 时取得最大值.若存在,求出
时取得最大值.若存在,求出 的前
的前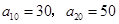 .
.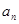 ;
;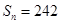 ,求
,求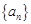 的前
的前 项和为
项和为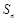 ,
,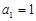 ,
, 是
是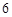 与
与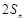 的等差中项(
的等差中项(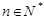 ).
).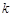 ,使不等式
,使不等式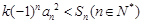 恒成立,若存在,求出
恒成立,若存在,求出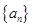 中,
中,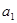 =1,当
=1,当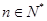 ,
,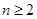 时,
时, =
= ,则数列
,则数列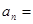 __________
__________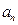 }的前
}的前 项和为
项和为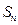 = n2 + 2n ,则数列{
= n2 + 2n ,则数列{