题目内容
已知等差数列{an}中,a1=1,a3=-3.
(1)求数列{an}的通项公式;
(2)若数列{an}的前k项和Sk=-35,求k的值.
(1) an=3-2n;(2) k=7.
解析试题分析:(1) 由于数列{an}是等差数列,又因为a1=1,a3=-3 ,所以其公差d=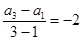 ,从而由等差数列的通项公式an=a1+(n-1)d 就可写出数列{an}的通项公式;(2)由(1)就可由等差数列的前n项和公式
,从而由等差数列的通项公式an=a1+(n-1)d 就可写出数列{an}的通项公式;(2)由(1)就可由等差数列的前n项和公式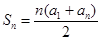 求出其前n项和,再由Sk=-35得到关于k的方程,解此方程可得k值;注意k∈N*.
求出其前n项和,再由Sk=-35得到关于k的方程,解此方程可得k值;注意k∈N*.
试题解析:(1)设等差数列{an}的公差为d,则an=a1+(n-1)d.
由a1=1,a3=-3,可得1+2d=-3,解得d=-2.
从而an=1+(n-1)×(-2)=3-2n.
(2)由(1)可知an=3-2n,
所以Sn=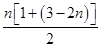 =2n-n2.由Sk=-35,可得2k-k2=-35,
=2n-n2.由Sk=-35,可得2k-k2=-35,
即k2-2k-35=0,解得k=7或k=-5.又k∈N*,故k=7.
考点:等差数列.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 中,
中, ,
,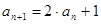 ,求
,求 .
. }、{
}、{ 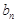 }满足:
}满足: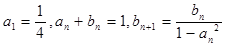 .
.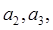
 }为等差数列,并求数列
}为等差数列,并求数列 和{
和{ 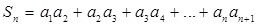 ,求实数
,求实数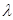 为何值时
为何值时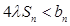 恒成立.
恒成立. 中,
中,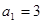 ,其前
,其前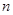 项和为
项和为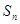 ,等比数列
,等比数列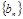 的各项均为正数,
的各项均为正数,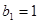 ,公比为
,公比为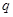 ,且
,且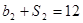 ,
,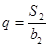 .
.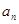 与
与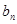 ; (2)设数列
; (2)设数列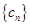 满足
满足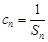 ,求
,求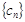 的前
的前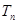 .
.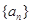 的公差
的公差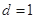 ,前
,前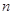 项和为
项和为 .
.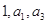 成等比数列,求
成等比数列,求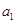 ;(2)若
;(2)若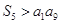 ,求
,求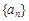 的前n项和为
的前n项和为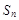 ,且
,且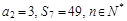
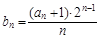 ,求数列
,求数列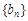 的前n项和Tn.
的前n项和Tn. 是数列
是数列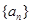 的前
的前 项和,且
项和,且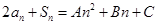 .
.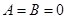 ,
,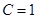 时,求
时,求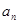 ;
; 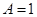 ,
,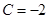 .
.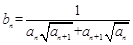 ,且数列
,且数列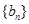 的前
的前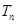 ,求
,求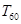 的值.
的值. 的前
的前 项和
项和 ,数列
,数列 满足
满足 .
.
 ,数列
,数列 的前
的前 ,求满足
,求满足 的
的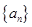 是等差数列,满足
是等差数列,满足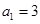 ,
, ,数列
,数列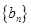 满足
满足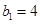 ,
,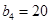 ,且
,且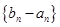 是等比数列.
是等比数列.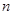 项和.
项和.