题目内容
已知数列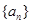 是等差数列,
是等差数列,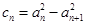 (
( ).
).
(Ⅰ)判断数列 是否是等差数列,并说明理由;
是否是等差数列,并说明理由;
(Ⅱ)如果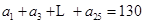 ,
, (
( 为常数),试写出数列
为常数),试写出数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,若数列 得前
得前 项和为
项和为 ,问是否存在这样的实数
,问是否存在这样的实数 ,使
,使 当且仅当
当且仅当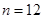 时取得最大值.若存在,求出
时取得最大值.若存在,求出 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(Ⅰ)数列 是等差数列;(Ⅱ)
是等差数列;(Ⅱ)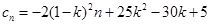 ;(Ⅲ)
;(Ⅲ)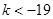 或
或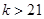 .
.
解析试题分析:(Ⅰ)等差数列的证明一般是从定义出发,注意若用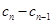 为常数,则需
为常数,则需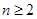 且
且 ;若用若用
;若用若用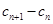 则
则 为常数,则需
为常数,则需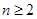 .(Ⅱ)因为
.(Ⅱ)因为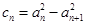 ,所以求数列
,所以求数列 的通项公式,关键是先求出等差数列
的通项公式,关键是先求出等差数列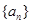 的通项公式,即求出
的通项公式,即求出 ,这样就必须建立关于
,这样就必须建立关于 的两个方程,求出
的两个方程,求出 ,显然必须从条件提供的两个等式出发去求解,注意求解的技巧;(Ⅲ)关于等差数列前
,显然必须从条件提供的两个等式出发去求解,注意求解的技巧;(Ⅲ)关于等差数列前 项和的最值问题,通常有两个思路,其一,从求和公式考虑,因为求和公式是关于
项和的最值问题,通常有两个思路,其一,从求和公式考虑,因为求和公式是关于 的二次式,可以结合二次函数知识解决问题,但要注意数列自身的特点,即
的二次式,可以结合二次函数知识解决问题,但要注意数列自身的特点,即 ;其二,从通项考虑,看何时变号.此题从通项考虑比较好.
;其二,从通项考虑,看何时变号.此题从通项考虑比较好.
试题解析:(Ⅰ)设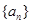 的公差为
的公差为 ,则
,则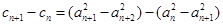

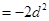
 数列
数列 是以
是以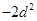 为公差的等差数列.
为公差的等差数列.
(Ⅱ)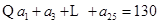

 两式相减:
两式相减: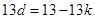
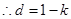
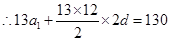 ,
,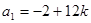
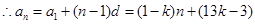

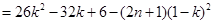
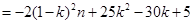
(Ⅲ)因为当且仅当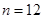 时
时 最大
最大 有
有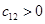 ,
,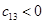 ,
,
即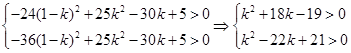
由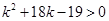 解得
解得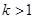 或
或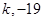 ;由
;由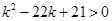 解得
解得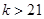 或
或 ,
,
综合得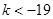 或
或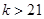 .
.
考点:等差数列的定义及求和、求通项.

练习册系列答案
相关题目
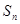 是等差数列
是等差数列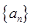
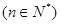 的前
的前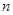 项和,且
项和,且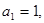
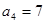 ,则
,则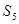 =
=  }、{
}、{ 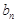 }满足:
}满足: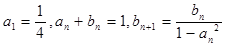 .
.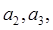
 }为等差数列,并求数列
}为等差数列,并求数列 和{
和{ 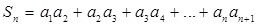 ,求实数
,求实数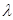 为何值时
为何值时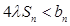 恒成立.
恒成立. }中,
}中, =14,前10项和
=14,前10项和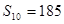 .
.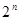 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前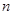 项和
项和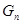 .
.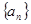 中,
中,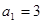 ,其前
,其前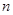 项和为
项和为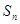 ,等比数列
,等比数列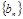 的各项均为正数,
的各项均为正数,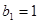 ,公比为
,公比为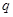 ,且
,且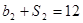 ,
,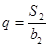 .
.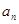 与
与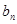 ; (2)设数列
; (2)设数列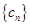 满足
满足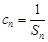 ,求
,求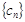 的前
的前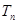 .
.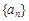 的前n项和为
的前n项和为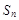 ,且
,且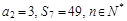
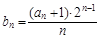 ,求数列
,求数列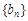 的前n项和Tn.
的前n项和Tn.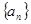 中,
中,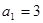 ,其前
,其前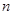 项和为
项和为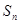 ,等比数列
,等比数列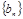 的各项均为正数,
的各项均为正数,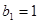 ,公比为
,公比为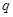 ,且
,且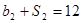 ,
,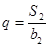 .
.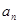 与
与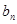 ; (2)设数列
; (2)设数列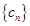 满足
满足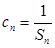 ,求
,求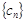 的前
的前 .
.
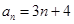 ,则数列{an}是公差为 的等差数列.
,则数列{an}是公差为 的等差数列.