题目内容
等差数列 的前
的前 项和记为
项和记为 ,已知
,已知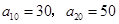 .
.
(1)求通项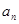 ;
;
(2)若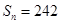 ,求
,求 .
.
(1) ;(2)n=11.
;(2)n=11.
解析试题分析:(1)首先设等差数列的首项和公差,再由等差数列的通项公式及已知条件可列出:关于首项和公差的二元一次方程组,解此方程组就可求得首项和公差,从而就可写出通项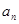 ;(2)由等差数列的前项和公式
;(2)由等差数列的前项和公式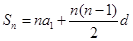 ,由(1)的结论和已知条件可得关于n的一个方程,解此方程就可求得n的值,注意n应为正整数即可.
,由(1)的结论和已知条件可得关于n的一个方程,解此方程就可求得n的值,注意n应为正整数即可.
试题解析:(1)由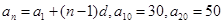 ,
,
得方程组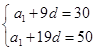 , 2分
, 2分
解得 , 4分
, 4分
所以 ; 5分
; 5分
(2)由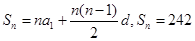 ,得方程
,得方程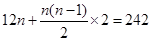 , 8分
, 8分
解得n=11或n=-22(舍去)。 10分
考点:等差数列的通项与前n项和公式.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
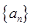 中,
中,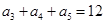 ,那么
,那么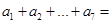
 }、{
}、{ 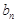 }满足:
}满足: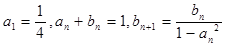 .
.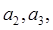
 }为等差数列,并求数列
}为等差数列,并求数列 和{
和{ 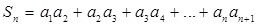 ,求实数
,求实数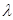 为何值时
为何值时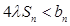 恒成立.
恒成立.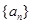 的前
的前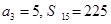 .
.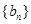 满足:
满足: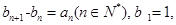 求数列
求数列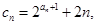 求数列
求数列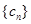 的前
的前
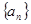 中,
中,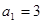 ,其前
,其前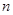 项和为
项和为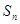 ,等比数列
,等比数列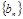 的各项均为正数,
的各项均为正数,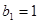 ,公比为
,公比为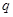 ,且
,且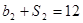 ,
,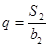 .
.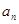 与
与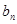 ; (2)设数列
; (2)设数列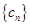 满足
满足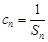 ,求
,求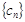 的前
的前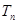 .
.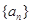 的公差
的公差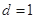 ,前
,前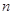 项和为
项和为 .
.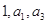 成等比数列,求
成等比数列,求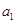 ;(2)若
;(2)若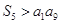 ,求
,求 是数列
是数列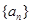 的前
的前 项和,且
项和,且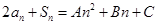 .
.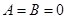 ,
,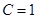 时,求
时,求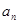 ;
; 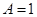 ,
,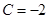 .
.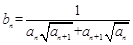 ,且数列
,且数列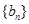 的前
的前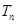 ,求
,求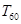 的值.
的值.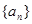 的前
的前 项和为
项和为 ,且
,且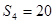 ,
,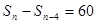 ,
,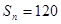 ,则
,则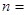 .
.