题目内容
【题目】已知二次函数![]()
(Ⅰ)若函数在区间![]() 上存在零点,求实数
上存在零点,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)问:是否存在常数![]() ,当
,当![]() 时,
时, ![]() 的值域为区间
的值域为区间![]() ,且
,且![]() 的长度为
的长度为![]() .(说明:对于区间
.(说明:对于区间![]() ,称
,称![]() 为区间长度)
为区间长度)
【答案】(1)![]() (2)存在常数
(2)存在常数![]() ,
, ![]() ,
, ![]() 满足题意.
满足题意.
【解析】试题分析:(1) 先由函数对称轴为![]() 得函数在
得函数在![]() 上单调减,要使函数在
上单调减,要使函数在![]() 存在零点,则需满足
存在零点,则需满足![]() ,解得
,解得![]() ; (2)当
; (2)当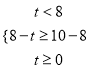 时,
时, ![]() 的值域为
的值域为![]() ,由
,由![]() ,得
,得![]() 合题意;当
合题意;当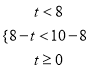 时,
时, ![]() 的值域为
的值域为![]() ,由
,由![]() ,得不合题意;当
,得不合题意;当![]() 时,
时, ![]() 的值域为
的值域为![]() ,用上面的方法得
,用上面的方法得![]() 或
或![]() 合题意.
合题意.
试题解析:⑴ ∵二次函数![]() 的对称轴是
的对称轴是![]()
∴函数![]() 在区间
在区间![]() 上单调递减
上单调递减
∴要函数![]() 在区间
在区间![]() 上存在零点须满足
上存在零点须满足![]()
即![]()
解得![]() ,所以
,所以![]() .
.
⑵ 当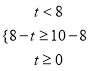 时,即
时,即![]() 时,
时, ![]() 的值域为:
的值域为: ![]() ,即
,即![]()
∴![]()
∴![]() ∴
∴![]()
经检验![]() 不合题意,舍去。
不合题意,舍去。
当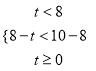 时,即
时,即![]() 时,
时, ![]() 的值域为:
的值域为: ![]() ,即
,即![]()
∴![]() , ∴
, ∴![]()
经检验![]() 不合题意,舍去。
不合题意,舍去。
当![]()
![]() 时,
时, ![]() 的值域为:
的值域为: ![]() ,即
,即![]()
∴![]()
∴![]() ∴
∴![]() 或
或![]()
经检验![]() 或
或![]() 或
或![]() 满足题意。
满足题意。
所以存在常数![]() ,当
,当![]() 时,
时, ![]() 的值域为区间
的值域为区间![]() ,且
,且![]() 的长度为
的长度为![]() .
.

练习册系列答案
相关题目
【题目】下表给出![]() 三种食物的维生素含量及其成本:
三种食物的维生素含量及其成本:
|
|
| |
维生素A(单位/千克) | 4000 | 5000 | 300 |
维生素B(单位/千克) | 700 | 100 | 300 |
成本(元/千克) | 6 | 4 | 3 |
现欲将三种食物混合成本100千克的混合食品,要求至少含35000单位维生素A,40000单位维生素B,采用何种配比成本最小?