Question

【题目】如图所示，直线PQ与⊙O切于点A，AB是⊙O的弦，∠PAB的平分线AC交⊙O于点C，连接CB，并延长与直线PQ相交于Q点．

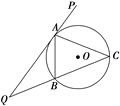
(1)求证：QC·AC＝QC2－QA2；

(2)若AQ＝6，AC＝5，求弦AB的长．

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）因为PQ与⊙O相切于点A，所以∠PAC＝∠CBA＝∠BAC，所以AC＝BC. 由割线定理得：QA2＝QB·QC＝(QC－BC)QC，所以QC·BC＝QC2－QA2，所以QC·AC＝QC2－QA2.（2）由条件，求出QC＝9，又△QAB∽△QCA，求出AB＝.

试题解析：

(1)证明：因为PQ与⊙O相切于点A，

所以∠PAC＝∠CBA，

因为∠PAC＝∠BAC，

所以∠BAC＝∠CBA，

所以AC＝BC.

由割线定理得：QA2＝QB·QC＝(QC－BC)QC，

所以QC·BC＝QC2－QA2，

所以QC·AC＝QC2－QA2.

(2)解：由AC＝BC＝5，AQ＝6及(1)知，QC＝9，

由∠QAB＝∠ACQ知△QAB∽△QCA，

所以＝，

所以AB＝.