Question

【题目】下表给出三种食物的维生素含量及其成本：

维生素A（单位/千克）	4000	5000	300
维生素B（单位/千克）	700	100	300
成本（元/千克）	6	4	3

现欲将三种食物混合成本100千克的混合食品，要求至少含35000单位维生素A，40000单位维生素B，采用何种配比成本最小？

Answer 1

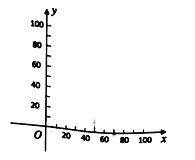
【答案】三种食物分别为30千克，10千克，60千克时成本最小

【解析】试题分析：应用问题首先要认真细致的审题，逐字逐句的读题，把实际问题转化为数学问题.本题为线性规划应用题，设出三种食物的重量x,y,z千克，根据题目的要求，列出二元一次不等式组，写出目标函数，利用简单的线性规划解题方法，作出可行域，找出最优解，求出目标函数的最小值，给出答案.

试题解析：

解：设三种食物分别用千克， 千克， 千克，

则满足 ，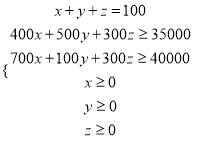

再设成本为元，则，

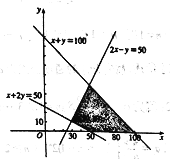
约束条件可转化为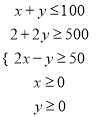

目标函数可转化为，

作出上面不等式组表示的平面区域，求得最优解为，

从而元，

答：三种食物分别却30千克，10千克，60千克时成本最小.