题目内容
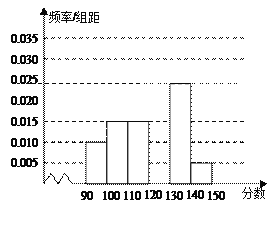
【题目】某校从参加高二某次月考的学生中随机抽取60名学生,将其数学成绩(均为整数)分成六组![]() 后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
后得到如右所示的部分频率分布直方图。观察图形信息,回答下列问题:
(Ⅰ)求分数在![]() 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在分数段![]() 的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段
的学生中抽取一个容量为6的样本,再从该样本中任取2人,求至多有1人在分数段![]() 内的概率。
内的概率。
【答案】(1)0.3(2)![]()
【解析】试题分析:(Ⅰ)根据频率分别直方图的面积表示频率,并且所以小矩形的面积之和等于![]() ,来求
,来求![]() 的面积,就是频率;(Ⅱ)第一步,先跟两个分数段的频率
的面积,就是频率;(Ⅱ)第一步,先跟两个分数段的频率![]() ,就是两个分数段的学生人数,第二步,计算分层比,计算两个分数段的各应抽取的人数,第三步,将这所抽取到的人分别编号,然后列举所有抽取到的组合情况,至多有1人在分数段[120,130)内组合数,按古典概型计算概率.
,就是两个分数段的学生人数,第二步,计算分层比,计算两个分数段的各应抽取的人数,第三步,将这所抽取到的人分别编号,然后列举所有抽取到的组合情况,至多有1人在分数段[120,130)内组合数,按古典概型计算概率.
试题解析:(Ⅰ)[120,130)内的频率为![]() ;…5分
;…5分
(Ⅱ)由题意,[110,120)分数段的人数为60×0.15=9(人).[120,130)分数段的人数为60×0.3=18(人).
∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本,
∴需在[110,120)分数段内抽取2人,并分别记为![]() 、
、![]() ;
;
在[120,130)分数段内抽取4人,并分别记为![]() 、
、![]() 、
、![]() 、
、![]() ;
;
设“从样本中任取2人,至多有1人在分数段[120,130)内”为事件A,则基本事件共有![]() ,
, ![]() 共15种.
共15种.
则事件A包含的基本事件有![]() ,
, ![]() 共9种.
共9种.
∴![]() .
.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目