题目内容
已知函数 .
.
(1)讨论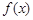 的单调性;
的单调性;
(2)设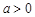 ,证明:当
,证明:当 时,
时,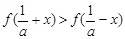 ;
;
(3)若函数 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分)
(1)若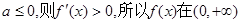 单调增加.
单调增加.
若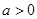 ,
,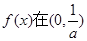 单调增加,在
单调增加,在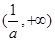 单调减少.
单调减少.
(2)见解析。
解析试题分析:解:(1)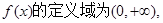 …………………………………………1分
…………………………………………1分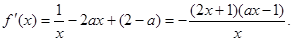 …………………………2分
…………………………2分
(i)若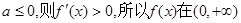 单调增加.…………………3分
单调增加.…………………3分
(ii)若
且当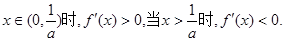
所以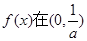 单调增加,在
单调增加,在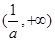 单调减少. ……………………5分
单调减少. ……………………5分
(2)设函数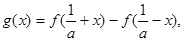 则
则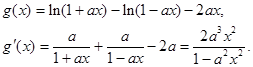
…………………………………7分
当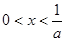 时,
时,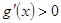 ,所以
,所以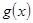 单调递增,
单调递增,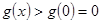
故当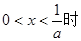 ,
,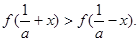 ……………………………9分
……………………………9分
(3)由(I)可得,当 的图像与x轴至多有一个交点,
的图像与x轴至多有一个交点,
故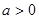 ,从而
,从而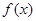 的最大值为
的最大值为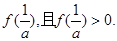
不妨设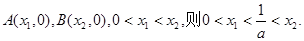
由(II)得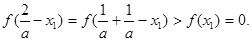
从而
由(I)知,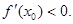 …………………………………………………14分
…………………………………………………14分
考点:本题考查利用导数求函数的单调性、综合分析和解决问题的能力以及分类讨论的思想方法。
点评:解答本题易出现以下失误:①忘记求函数的定义域;②想不到分类讨论,从而在判断函数的单调性时出现错误。当求函数的单调性时,如果无法判断导函数的符号,自然而然的就应该想到分类讨论,为了避免错误的发生,在平常做题时就要养成分析思路的习惯。

练习册系列答案
相关题目
 为实数,函数
为实数,函数 ,
, .
. 的单调区间与极值;
的单调区间与极值; 且
且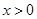 时,
时, .
. (单位:m/s)紧急刹车至停止。求:
(单位:m/s)紧急刹车至停止。求: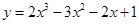 ,过点
,过点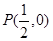 的切线方程为
的切线方程为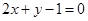 ,且交于曲线
,且交于曲线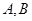 两点,求切线
两点,求切线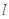 与C围成的图形的面积。
与C围成的图形的面积。 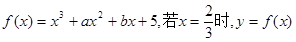 有极值,且曲线
有极值,且曲线 处的切线斜率为3.
处的切线斜率为3. 的解析式;
的解析式; 在
在 上的最大值和最小值.
上的最大值和最小值. ,
, .
. 时,求函数
时,求函数 的极值点;
的极值点; 的单调区间上也是单调的,求
的单调区间上也是单调的,求 的取值范围;
的取值范围; 时,设
时,设 ,且
,且 是函数
是函数 的极值点,证明:
的极值点,证明: .
.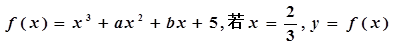 有极值,且曲线
有极值,且曲线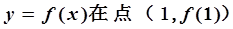 处的切线斜率为3.
处的切线斜率为3.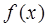 的解析式;
的解析式;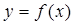 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。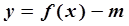 有三个零点,求实数
有三个零点,求实数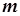 的取值范围.
的取值范围.
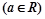 .
.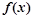 的单调区间;
的单调区间;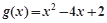 ,若对任意
,若对任意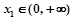 ,均存在
,均存在 ,使得
,使得 ,求a的取值范围.
,求a的取值范围. 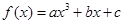
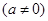 为奇函数,其图象在点
为奇函数,其图象在点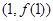 处的切线与直线
处的切线与直线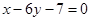 垂直,导函数
垂直,导函数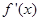 的最小值为
的最小值为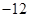 .试求
.试求 ,
,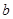 ,
,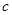 的值。
的值。