题目内容
(12分)设 为实数,函数
为实数,函数 ,
, .
.
(1)求 的单调区间与极值;
的单调区间与极值;
(2)求证:当 且
且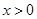 时,
时, .
.
(1)单调递减区间是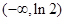 ,单调递增区间是
,单调递增区间是 ,极小值为
,极小值为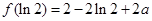 (2)设
(2)设 ,于是
,于是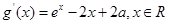 ,
, 取最小值为
取最小值为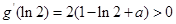
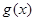 在R内单调递增,有
在R内单调递增,有 ,而
,而 ,有
,有 故
故
解析试题分析:(Ⅰ)解:由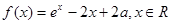 知
知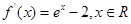 。 …2分
。 …2分
令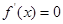 ,得
,得 。于是,当
。于是,当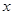 变化时,
变化时,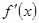 和
和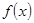 的变化情况如下表:
的变化情况如下表:
……………………………4分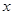
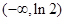



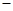
0 + 
单调递减 
单调递增
故 的单调递减区间是
的单调递减区间是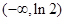 ,单调递增区间是
,单调递增区间是 。
。 在
在 处取得极小值。极小值为
处取得极小值。极小值为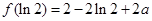 ……………6分
……………6分
(Ⅱ)证明:设 ,于是
,于是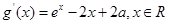 。
。
由(Ⅰ)知当 时
时 取最小值为
取最小值为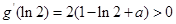
于是对任意 ,都有
,都有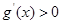 ,所以
,所以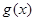 在R内单调递增。 ……8分
在R内单调递增。 ……8分
于是,当 时,对任意
时,对任意 ,都有
,都有 ,而
,而 ………10分
………10分
从而对任意 ,都有
,都有 。即
。即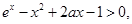 故
故 12分
12分
考点:函数单调区间极值及利用单调性最值证明不等式
点评:证明不等式恒成立问题常转化为求函数最值问题

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 在
在 处取得极值,并且它的图象与直线
处取得极值,并且它的图象与直线 在点( 1 , 0 ) 处相切, 求a , b , c的值.
在点( 1 , 0 ) 处相切, 求a , b , c的值. .
. 在区间
在区间 上是增函数还是减函数?证明你的结论;
上是增函数还是减函数?证明你的结论; 时,
时, 恒成立,求整数
恒成立,求整数 的最大值;
的最大值; .
.
 时,求函数
时,求函数 的单调区间;
的单调区间; 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为 ,问:
,问: 在什么范围取值时,对于任意的
在什么范围取值时,对于任意的 ,函数
,函数 在区间
在区间 上总存在极值?
上总存在极值?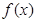


 ,
, 的值;
的值; 的最小值。
的最小值。 )
)
 上是单调函数,求
上是单调函数,求 的取值范围。
的取值范围。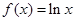 ,
,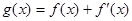 .
.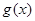 的单调区间和最小值;
的单调区间和最小值;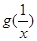 的大小关系;
的大小关系;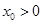 ,使得
,使得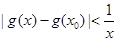 对任意
对任意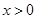 成立?若存在,求出
成立?若存在,求出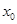 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.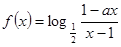 为奇函数,a为常数。
为奇函数,a为常数。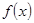 在区间
在区间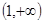 上为增函数;
上为增函数; 上的每一个
上的每一个 的值,不等式
的值,不等式 恒成立,求实数m 的取值范围。
恒成立,求实数m 的取值范围。 ,
, 的单调区间;(II)求
的单调区间;(II)求 上的最小值。
上的最小值。 .
.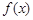 的单调性;
的单调性;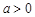 ,证明:当
,证明:当 时,
时,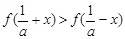 ;
; 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明: (x0)<0.(本题满分14分)
(x0)<0.(本题满分14分)