题目内容
11. 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )| A. | x2+y2+xy-1=0 | B. | x2+y2+xy+1=0 | C. | x2+y2-xy-1=0 | D. | x2+y2-xy+1=0 |
分析 过P作PA⊥x,PB⊥y,设P(x,y)在直角坐标系下的坐标为P′(x0,y0),建立P′(x0,y0)与P(x,y)的坐标关系即可得到结论.
解答 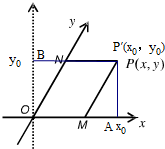 解:过P作PA⊥x,PB⊥y,
解:过P作PA⊥x,PB⊥y,
设P(x,y)在直角坐标系下的坐标为P′(x0,y0),
∵∠BON=30°,ON=y,
∴OB=$\frac{\sqrt{3}}{2}$y,BN=$\frac{1}{2}y$,
即y0=$\frac{\sqrt{3}}{2}$y,x0=x+$\frac{1}{2}y$,
∵P′(x0,y0)在单位圆x2+y2=1上,
∴x02+y02=1,
即($\frac{\sqrt{3}}{2}$y)2+(x+$\frac{1}{2}y$)2=1,
整理得x2+y2+xy-1=0,
故选:A.
点评 本题主要考查与直角坐标系有关的新定义问题,根据条件求出P′(x0,y0)与P(x,y)的坐标关系是解决本题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
2.随机变量X的概率分布如下:
则E(X)=2.6.
| X | 1 | 2 | 3 | 4 |
| P | 0.2 | 0.3 | p | 0.3 |
6.已知数列﹛an﹜满足an+1=$\frac{1}{2}+\sqrt{{a_n}-a_n^2}$,且a1=$\frac{1}{2}$,则该数列前2013项和等于( )
| A. | 1509.5 | B. | 1508.5 | C. | 1509 | D. | 1508 |
3.在△ABC中,∠A、B、C对边分别为a、b、c,A=60°,b=1,这个三角形的面积为$\sqrt{3}$,则△ABC外接圆的直径是( )
| A. | $\sqrt{39}$ | B. | $\frac{\sqrt{39}}{3}$ | C. | $\frac{\sqrt{39}}{6}$ | D. | $\frac{2\sqrt{39}}{3}$ |
1.甲乙两人独立的解同一道题,甲乙解对的概率分别是p1,p2,那么至少有1人解对的概率是( )
| A. | p1+p2 | B. | p1•p2 | C. | 1-p1•p2 | D. | 1-(1-p1)•(1-p2) |
 如图3,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图3,正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论: 设OADB是平行四边形,其对角线相交于C点,$\overrightarrow{BM}$=$\frac{1}{3}$$\overrightarrow{BC}$,$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$,
设OADB是平行四边形,其对角线相交于C点,$\overrightarrow{BM}$=$\frac{1}{3}$$\overrightarrow{BC}$,$\overrightarrow{CN}$=$\frac{1}{3}$$\overrightarrow{CD}$,