题目内容
19.一球内切于棱长为2的正方体,则该球的体积为$\frac{4}{3}π$该球表面积为4π.分析 因为球内切与正方体,所以求导直径与正方体的棱长相等,得到球的半径,利用公式求体积和表面积.
解答 解:因为球内切于棱长为2的正方体,所以球的直径等于正方体的棱长,所以球的半径为1,
所以该球的体积为$\frac{4π}{3}$,该球表面积为4π;
故答案为:$\frac{4}{3}π$;4π.
点评 本题考查了正方体的内切球的体积、表面积求法;关键是明确球的直径与正方体的棱长相等.

练习册系列答案
相关题目
10.定义:分子为1且分母为正整数的分数称为单位分数.我们可以把1分拆为若干个不同的单位分数之和.如:1=$\frac{1}{2}+\frac{1}{3}+\frac{1}{6}$,1=$\frac{1}{2}+\frac{1}{4}+\frac{1}{6}+\frac{1}{12}$,1=$\frac{1}{2}+\frac{1}{5}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}$,
依此类推可得:1=$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{13}+\frac{1}{n}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}+\frac{1}{156}$,其中n∈N*.设1≤x≤13,1≤y≤n,则$\frac{x+y+2}{x+1}$的最小值为( )
依此类推可得:1=$\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{13}+\frac{1}{n}+\frac{1}{30}+\frac{1}{42}+\frac{1}{56}+\frac{1}{72}+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}+\frac{1}{156}$,其中n∈N*.设1≤x≤13,1≤y≤n,则$\frac{x+y+2}{x+1}$的最小值为( )
| A. | $\frac{23}{2}$ | B. | $\frac{8}{7}$ | C. | $\frac{5}{2}$ | D. | $\frac{34}{3}$ |
11.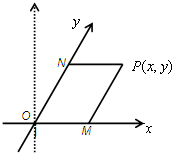 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )
 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )| A. | x2+y2+xy-1=0 | B. | x2+y2+xy+1=0 | C. | x2+y2-xy-1=0 | D. | x2+y2-xy+1=0 |
8.在△ABC中,∠A、B、C对边分别为a、b、c,A=60°,b=1,这个三角形的面积为$\sqrt{3}$,则a=( )
| A. | 2 | B. | $\sqrt{10}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{13}$ |
 如图所示,墙上挂有边长为a的正方形木板,它的四个角的阴影部分都是以正方形的顶点为圆心,半径为$\frac{a}{2}$的圆弧.某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都相等,此人投镖4000次,镖击中空白部分的次数是854次.据此估算:圆周率π约为3.146.
如图所示,墙上挂有边长为a的正方形木板,它的四个角的阴影部分都是以正方形的顶点为圆心,半径为$\frac{a}{2}$的圆弧.某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都相等,此人投镖4000次,镖击中空白部分的次数是854次.据此估算:圆周率π约为3.146.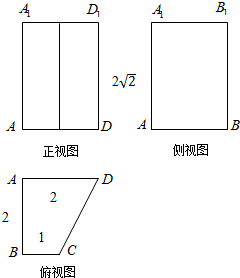 已知四棱柱ABCD-A1B1C1D1的三视图如图所示.
已知四棱柱ABCD-A1B1C1D1的三视图如图所示.