题目内容
16.在直角坐标系xOy中,直线l过抛物线y2=4x的焦点F且与该抛物线交于A、B两点.其中点A在x轴上方.若直线l的倾斜角为60°.则△OAB的面积为$\frac{4\sqrt{3}}{3}$.分析 通过题意易知直线l方程为:$\sqrt{3}x-y-\sqrt{3}=0$,利用韦达定理、两点间距离公式可知|AB|=$\frac{16}{3}$,结合点到直线的距离公式、三角形面积公式计算即得结论.
解答 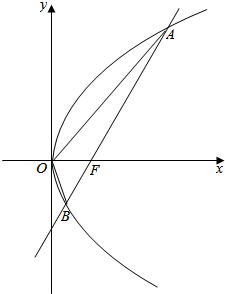 解:∵抛物线方程为:y2=4x,
解:∵抛物线方程为:y2=4x,
∴F(1,0),
又∵直线l的倾斜角为60°,
∴直线l的斜率k=tan60°=$\sqrt{3}$,
∴直线l方程为:y=$\sqrt{3}$(x-1),即$\sqrt{3}x-y-\sqrt{3}=0$,
联立$\left\{\begin{array}{l}{y=\sqrt{3}(x-1)}\\{{y}^{2}=4x}\end{array}\right.$,
消去y整理得:3x2-10x+3=0,
∴xA+xB=$\frac{10}{3}$,xAxB=1,
∴yA-yB=[$\sqrt{3}$(xA-1)]-[$\sqrt{3}$(xB-1)]=$\sqrt{3}$(xA-xB),
∴|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({{y}_{A}-y}_{B})^{2}}$
=$\sqrt{({x}_{A}-{x}_{B})^{2}+3({{x}_{A}-{x}_{B})}^{2}}$
=2$\sqrt{({x}_{A}+{x}_{B})^{2}-4{x}_{A}{x}_{B}}$
=2$\sqrt{({\frac{10}{3})}^{2}-4}$
=$\frac{16}{3}$,
又∵原点O到直线AB的距离d=$\frac{|0-0-\sqrt{3}|}{\sqrt{({\sqrt{3})}^{2}+(-1)^{2}}}$=$\frac{\sqrt{3}}{2}$,
∴S△OAB=$\frac{1}{2}$•|AB|•d=$\frac{1}{2}•$$\frac{16}{3}$•$\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$,
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题考查抛物线的简单性质,考查数形结合,注意解题方法的积累,属于中档题.

 如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )
如图,将平面直角坐标系中的纵轴绕原点O顺时针旋转30°后,构成一个斜坐标平面xOy.在此斜坐标平面xOy中,点P(x,y)的坐标定义如下:过点P作两坐标轴的平行线,分别交两轴于M、N两点,则M在Ox轴上表示的数为x,N在Oy轴上表示的数为y.那么以原点O为圆心的单位圆在此斜坐标系下的方程为( )| A. | x2+y2+xy-1=0 | B. | x2+y2+xy+1=0 | C. | x2+y2-xy-1=0 | D. | x2+y2-xy+1=0 |
| A. | 2 | B. | $\sqrt{10}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{13}$ |
 如图,在圆内:画1条弦,把圆分成2部分:画2条相交的弦,把圆分成4部分,画3条两两相交的弦,把圆最多分成7部分….画5条两两相交的弦,把圆最多分成16部分:画n条两两相交的弦,把圆最多分成$\frac{{n}^{2}+n+2}{2}$部分.
如图,在圆内:画1条弦,把圆分成2部分:画2条相交的弦,把圆分成4部分,画3条两两相交的弦,把圆最多分成7部分….画5条两两相交的弦,把圆最多分成16部分:画n条两两相交的弦,把圆最多分成$\frac{{n}^{2}+n+2}{2}$部分. 已知四棱柱ABCD-A1B1C1D1的三视图如图所示.
已知四棱柱ABCD-A1B1C1D1的三视图如图所示.