题目内容
【题目】定义:如果数列![]() 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称![]() 为三角形”数列对于“三角形”数列
为三角形”数列对于“三角形”数列![]() ,如果函数
,如果函数![]() 使得
使得![]() 仍为一个三角形”数列,则称
仍为一个三角形”数列,则称![]() 是数列
是数列![]() 的“保三角形函数”
的“保三角形函数”![]() .
.
(1)已知![]() 是首项为2,公差为1的等差数列,若
是首项为2,公差为1的等差数列,若![]() ,
,![]() 是数列
是数列![]() 的保三角形函数”,求
的保三角形函数”,求![]() 的取值范围;
的取值范围;
(2)已知数列![]() 的首项为2019,
的首项为2019,![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足
项和,且满足![]() ,证明
,证明![]() 是“三角形”数列;
是“三角形”数列;
(3)求证:函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”的充要条件是
的“保三角形函数”的充要条件是![]() ,
,![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】
(1)先由条件得![]() 是三角形数列,再利用
是三角形数列,再利用![]() ,
,![]() 是数列
是数列![]() 的“保三角形函数”,得到
的“保三角形函数”,得到![]() ,解得
,解得![]() 的取值范围;
的取值范围;
(2)先利用条件求出数列![]() 的通项公式,再证明其满足“三角形”数列的定义即可;
的通项公式,再证明其满足“三角形”数列的定义即可;
(3)根据函数![]() ,
,![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”,可以得到①1,
的“保三角形函数”,可以得到①1,![]() ,
,![]() 是三角形数列,所以
是三角形数列,所以![]() ,即
,即![]() ,②数列中的各项必须在定义域内,即
,②数列中的各项必须在定义域内,即![]() ,③
,③![]() ,
,![]() ,
,![]() 是三角形数列;结论为在利用
是三角形数列;结论为在利用![]() ,
,![]() 是单调递减函数,就可求出对应
是单调递减函数,就可求出对应![]() 的范围,即可证明.
的范围,即可证明.
(1)解:显然![]() ,
,![]() 对任意正整数都成立,即
对任意正整数都成立,即![]() 是三角形数列,
是三角形数列,
因为![]() ,显然有
,显然有![]() ,
,
由![]() 得
得![]() ,解得
,解得![]() ,
,
所以当![]() 时,
时,![]() 是数列
是数列![]() 的“保三角形函数”;
的“保三角形函数”;
(2)证:由![]() ,
,
当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
当![]() 时,即
时,即![]() ,解得
,解得![]() ,∴
,∴![]() ,
,
∴数列![]() 是以2019为首项,以
是以2019为首项,以![]() 为公比的等比数列,
为公比的等比数列,
∴![]() ,
,
显然![]() ,因为
,因为![]()
![]()
![]() ,
,
所以![]() 是“三角形”数列;
是“三角形”数列;
(3)证:函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”,必须满足三个条件:
的“保三角形函数”,必须满足三个条件:
①1,![]() ,
,![]() 是三角形数列,所以
是三角形数列,所以![]() ,即
,即![]() ;
;
②数列中的各项必须在定义域内,即![]() ;
;
③![]() ,
,![]() ,
,![]() 是三角形数列,
是三角形数列,
由于![]() ,
,![]() 是单调递减函数,所以
是单调递减函数,所以![]() ,解得
,解得![]() ,
,
所以函数![]() ,
,![]() 是数列1,
是数列1,![]() ,
,![]() 的“保三角形函数”的充要条件是
的“保三角形函数”的充要条件是![]() ,
,![]() .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: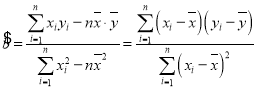 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)