题目内容
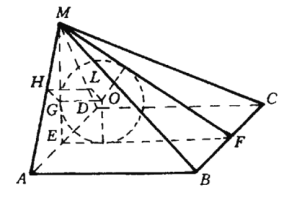
【题目】设棱锥M-ABCD的底面是正方形,且MA=MD,MA⊥AB.如果△AMD的面积为1,试求能够放入这个棱锥的最大球的半径.
【答案】![]()
【解析】
如图,因为AB⊥AD,AB⊥MA,所以,AB垂直于平面MAD,
由此知平面MAD垂直平面AC.
设E是AD的中点,F是BC的中点,则ME⊥AD,所以,ME垂直平面AC,ME⊥EF.
设球O是与平面MAD,AC,MBC都相切的球.
不失一般性,可设O在平面MEF上.于是O为△MEF的内心.
设球O的半径为r,则![]() .
.
设AD=EF=a,因为![]() ,所以
,所以![]() ,
,
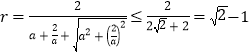 ,
,
且当![]() ,即
,即![]() 时,上式取等号,所以,当AD=ME=
时,上式取等号,所以,当AD=ME=![]() 时,
时,
与三个面MAD,AC,MBC都相切的球的半径最大,并且这个最大半径为![]() .
.
作OG⊥ME于G,易证OG//平面MAB,G到平面MAB的距离就是O到平面MAB的距离.
过G作MH⊥MA于H,则GH是G到平面MAB的距离.
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
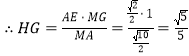 .
.
![]() ,
,
故O到平面MAB的距离大于球O的半径r,同样O到面MCD的距离也大于球O的半径r,
故球O在棱锥M-ABCD内,并且不可能再大.
据此可得所求的最大球的半径为![]() .
.

练习册系列答案
相关题目
