题目内容

已知函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，且当x＞0时，f（x）=log2x，g（x）=x2-3，那么函数y=f（x）g（x）的大致图象为（　　）
A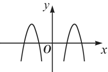．B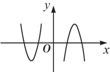．C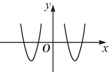．D．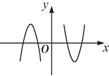
∵函数f（x）是定义在（-∞，0）∪（0，+∞）上的奇函数，
又∵g（x）=x2-3为偶函数，
∴函数y=f（x）g（x）为奇函数，其图象关于原点对称
故可排除A，C
又∵当x＞0时，f（x）=log2x，
∴当0＜x＜1时，y=f（x）g（x）＞0；当1＜x＜
3
时，y=f（x）g（x）＜0；当x＞
3
时，y=f（x）g（x）＞0
故可排除B
故选D
练习册系列答案
相关题目
（本小题满分12分） 已知函数
（Ⅰ）当时，求函数的值域（Ⅱ）若在上恒有意义，求实数的取值范围
设a=log
1
2
3，b=(
1
3
)-0.2，c=ln
3
2
，则a、b、c的大小关系为（　　）
A．b＜a＜cB．c＜b＜aC．a＜b＜cD．a＜c＜b
下列等式成立的是（　　）
A．log2（3÷5）=log23-log25B．log2（-10）2=2log2（-10）
C．log2（3+5）=log23•log25D．log2（-5）3=-log253
已知f（x）=ax-2，g（x）=loga|x|（a＞0且a≠1），若f（4）•g（-4）＜0，则y=f（x），y=g（x）在同一坐标系内的大致图象是（　　）
A．B．C．D．
已知函数y=f（x）（x∈R）满足f（x+3）=f（x+1）且当x∈[-1，1]时，f（x）=x2，则y=f（x）与y=log7x的图象的交点个数为（　　）
A．3B．4C．5D．6
已知a＞0且a≠1，f（logax）=x2+2x-1
（1）求f（x）的解析式和定义域；
（2）若函数f（x）在区间[-1，1]上的最大值是
31
9
，求实数a的值．
已知函数f（x）=㏒
1
2
（x2-ax-a）的值域为R，且f（x）在（-3，1-
3
）上是增函数，则a的取值范围是（　　）
A．0≤a≤2B．-
9
2
≤a≤-4		C．-4＜a＜0D．a＜0
已知函数f（x）=-x+log2
1-x
1+x

（1）求函数f（x）的定义域；
（2）求f（
1
2012
）+f（
1
2013
）+f（-
1
2012
）+f（-
1
2013
）的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网