题目内容
已知函数f(x)=㏒
(x2-ax-a)的值域为R,且f(x)在(-3,1-
)上是增函数,则a的取值范围是( )
| 1 |
| 2 |
| 3 |
| A.0≤a≤2 | B.-
| C.-4<a<0 | D.a<0 |
当a>0时,△=4a2+4a≥0,解得a≥0或a≤-1,
f(x)在(-3,1-
)上是增函数,
∴内层函数x2-ax-a在(-3,1-
)上是减函数
∵
≥1-
,且(x2-ax-a)|x=1-
≥0.
即a≥2-2
,且a≤2
综上知实数a的取值范围是0≤a≤2
故选A.
f(x)在(-3,1-
| 3 |
∴内层函数x2-ax-a在(-3,1-
| 3 |
∵
| a |
| 2 |
| 3 |
| 3 |
即a≥2-2
| 3 |
综上知实数a的取值范围是0≤a≤2
故选A.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
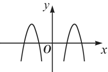
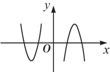
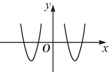
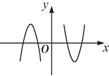
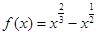 ,则满足
,则满足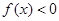 的
的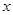 取值范围是 .
取值范围是 .