题目内容
已知函数f(x)=-x+log2
(1)求函数f(x)的定义域;
(2)求f(
)+f(
)+f(-
)+f(-
)的值.
| 1-x |
| 1+x |
(1)求函数f(x)的定义域;
(2)求f(
| 1 |
| 2012 |
| 1 |
| 2013 |
| 1 |
| 2012 |
| 1 |
| 2013 |
(1)由
>0,得(1-x)(1+x)>0,
解得:-1<x<1.
∴函数f(x)的定义域为(-1,1);
(2)函数f(x)的定义域为(-1,1),
又∵f(-x)=x+log2
=x-log2
=-f(x),
∴函数f(x)为奇函数,
即f(-x)+f(x)=0.
∴f(
)+f(
)+f(-
)+f(-
)=0
| 1-x |
| 1+x |
解得:-1<x<1.
∴函数f(x)的定义域为(-1,1);
(2)函数f(x)的定义域为(-1,1),
又∵f(-x)=x+log2
| 1+x |
| 1-x |
| 1-x |
| 1+x |
∴函数f(x)为奇函数,
即f(-x)+f(x)=0.
∴f(
| 1 |
| 2012 |
| 1 |
| 2013 |
| 1 |
| 2012 |
| 1 |
| 2013 |

练习册系列答案
相关题目
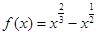 ,则满足
,则满足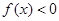 的
的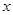 取值范围是 .
取值范围是 .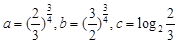 ,则
,则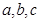 从小到大用“﹤”号排列为
从小到大用“﹤”号排列为