题目内容
【题目】已知[x)表示大于x的最小整数,例如[3)=4,[﹣1,3)=﹣1,下列命题中正确的是( ) ①函数f(x)=[x)﹣x的值域是(0,1]
②若{an}是等差数列,则{[an)}也是等差数列
③若{an}是等比数列,则{[an)}也是等比数列
④若x∈(1,2017),则方程[x)﹣x=sin ![]() x有1007个根.
x有1007个根.
A.②
B.③④
C.①
D.①④
【答案】D
【解析】解:对①,当x为整数时,[x)=x+1,即[x)﹣x=1,当x不为整数时,0<[x)﹣x<1,所以函数f(x)=[x)﹣x的 值域是(0,1]即①对; 对②,当数列{an}是整数构成的等差数列,则数列{[an)}也是等差数列;当{an}不是整数构成的等差数列,则数列{[an)}不是等差数列.
例如:数列{an}:0.4,0.5,0.6,0.7,0.8,0.9,1.0,1.1;那么数列
{[an)}:1,1,1,1,1,1,2,2显然不是等差数列.故②错;
对③,可取等比数列{an}:1,2,4,8,16;则数列{[an)}为:2,3,5,9,17显然不是等比数列,故③错;
对④,因为x∈(1,2017),函数f(x)=[x)﹣x=sin ![]() x的周期T=4,在(1,5]内有两个根,一个根x∈(4,5),另一个根x=5.因此方程[x)﹣x=sin
x的周期T=4,在(1,5]内有两个根,一个根x∈(4,5),另一个根x=5.因此方程[x)﹣x=sin ![]() x在区间(1,2017)内共有504×2﹣1=1007个根.
x在区间(1,2017)内共有504×2﹣1=1007个根.
故④对.
故选:D.
【考点精析】关于本题考查的等比数列的通项公式(及其变式),需要了解通项公式:![]() 才能得出正确答案.
才能得出正确答案.

【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
【题目】如表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表提供的数据,求出y关于x的线性回归方程为 ![]() =0.7x+0.35,则下列结论错误的是( )
=0.7x+0.35,则下列结论错误的是( )
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.产品的生产能耗与产量呈正相关
B.t的取值必定是3.15
C.回归直线一定过点(4,5,3,5)
D.A产品每多生产1吨,则相应的生产能耗约增加0.7吨
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |
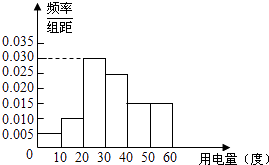
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.