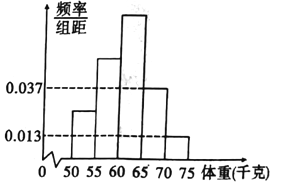
题目内容
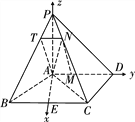
【题目】如图所示,四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() .
.
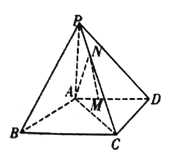
(1)证明: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值
所成角的正弦值
【答案】(1)详见解析;(2) ![]() .
.
【解析】试题分析:证明线面平行有两种思路:第一寻求线线平行,利用线面平行的判定定理.第二寻求面面平行,进而说明线面平行;本题借助平行四边形可以得到线线平行,进而证明线面平行;第二步求线面角,建立空间直角坐标系,写出相关点的坐标,借助空间向量,求法向量,利用公式求角.
试题解析:
(Ⅰ)证明:由已知得![]() ,如图,取
,如图,取![]() 上靠近
上靠近![]() 的四等分点
的四等分点![]() ,连接
,连接![]() ,
,
由![]() 知
知![]() ,
, ![]() .
.
又![]() ,故
,故![]() 平行且等于
平行且等于![]() ,四边形
,四边形![]() 为平行四边形,于是
为平行四边形,于是![]() .
.
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)解:如图,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
由![]() 得
得![]() ,从而
,从而![]() ,且
,且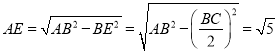 .
.
以![]() 为坐标原点,
为坐标原点, ![]() 的方向为
的方向为![]() 轴正方向,建立如图所示的空间直角坐标系
轴正方向,建立如图所示的空间直角坐标系![]() .
.
由题意知, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, 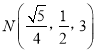 ,
,
![]() ,
, ![]() ,
, 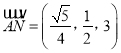 .
.
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则![]() 即
即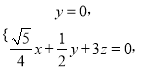
可取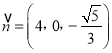 .于是
.于是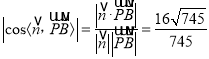 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
相关题目