题目内容
【题目】某市政府为了确定一个较为合理的居民用电标准,必须先了解全市居民日常用电量的分布情况.现采用抽样调查的方式,获得了n位居民在2012年的月均用电量(单位:度)数据,样本统计结果如下图表:
分 组 | 频 数 | 频 率 |
[0,10) | 0.05 | |
[10,20) | 0.10 | |
[20,30) | 30 | |
[30,40) | 0.25 | |
[40,50) | 0.15 | |
[50,60] | 15 | |
合 计 | n | 1 |
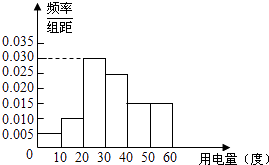
(1)求月均用电量的中位数与平均数估计值;
(2)如果用分层抽样的方法从这n位居民中抽取8位居民,再从这8位居民中选2位居民,那么至少有1位居民月均用电量在30至40度的概率是多少?
(3)用样本估计总体,把频率视为概率,从这个城市随机抽取3位居民(看作有放回的抽样),求月均用电量在30至40度的居民数X的分布列.
【答案】
(1)解:中位数估计值为32,
平均数估计值为0.05×5+0.1×15+0.3×25+0.25×35+0.15×45+0.15×55=33
(2)解:由 ![]() 得n=100,
得n=100,
抽取的8位居民中月均用电量在30至40度的居民有 ![]() 人,
人,
∴至少1位居民月均用电量在30至40度概率为 ![]()
(3)解:抽取1位居民月均用电量 在30至40度的概率为 ![]() ,
,
∴ ![]()
∴X的分布列为
x | 0 | 1 | 2 | 3 |
P |
|
|
|
|
【解析】(1)根据频率分布直方图,求月均用电量的中位数与平均数估计值;(2)先求出n,抽取的8位居民中月均用电量在30至40度的居民人数,即可求出至少有1位居民月均用电量在30至40度的概率;(3)X服从二项分布,即可求月均用电量在30至40度的居民数X的分布列.
【考点精析】通过灵活运用分层抽样和离散型随机变量及其分布列,掌握先将总体中的所有单位按照某种特征或标志(性别、年龄等)划分成若干类型或层次,然后再在各个类型或层次中采用简单随机抽样或系用抽样的办法抽取一个子样本,最后,将这些子样本合起来构成总体的样本;在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.