题目内容
18.某个体服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这件服装件数x之间的一组数据关系如表所示:| x | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 66 | 69 | 73 | 81 | 89 | 90 | 91 |
(Ⅰ)求$\overrightarrow{x}$,$\overrightarrow{y}$;
(Ⅱ)若纯利y与每天销售件数x之间的回归直线方程;
(Ⅲ)若该周内某天销售服装20件,估计可获纯利多少元?
分析 (Ⅰ)利用平均数公式,可求$\overrightarrow{x}$,$\overrightarrow{y}$;
(Ⅱ)求出利用最小二乘法来求线性回归方程的系数的量,求出横标和纵标的平均数,求出系数,再求出a的值;
(Ⅲ)由回归直线方程预测,只需将x=20代入求解即可.
解答 解:(Ⅰ)$\overline{x}$=$\frac{1}{7}$(3+4+5+6+7+8+9)=6,$\overrightarrow{y}$=$\frac{1}{7}$(66+69+73+81+89+90+91)=80,
(Ⅱ)∵$\sum_{i-1}^{7}$xi2=280,$\sum_{i-1}^{7}$xiyi=3487,
∴b=$\frac{3487-7×6×80}{280-7×36}$=$\frac{33}{7}$,a=$\frac{362}{7}$,
∴回归方程为y=$\frac{33}{7}$x+$\frac{362}{7}$,
(Ⅲ)当x=20时,y≈175,
故该周内某天的销售量为20件,估计这天可获纯利大约为175元.
点评 本题重点考查了平均值、线性回归直线方程及其求解过程,属于中档题,解题关键是记住回归系数的求解公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.如图所示的程序框图,若输出的S是62,则①可以为( )
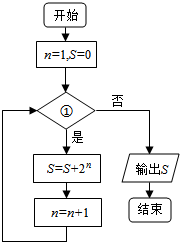

| A. | n≤3? | B. | n≤4? | C. | n≤5? | D. | n≤6? |
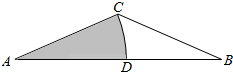 如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.
如图,在一个等腰三角形ABC内以A为圆心,腰AC长为半径画弧交底边AB于D,已知AC=1,∠A=30°,现向△ABC内任投一点,该点落在图中阴影部分的概率为$\frac{\sqrt{3}π}{9}$.