Question

【题目】已知椭圆： ，其中， 为左、右焦点，且离心率，直线与椭圆交于两不同点， .当直线过椭圆右焦点且倾斜角为时，原点到直线的距离为.

[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/12/1922378615128064/1923439395913728/STEM/2d7d70ba831f438cb4e191e234d85c18.png]

（Ⅰ）求椭圆的方程；

（Ⅱ）若，当面积为时，求的最大值.

Answer 1

【答案】(Ⅰ) ；(Ⅱ)5.

【解析】试题分析：（Ⅰ）本题考察的是椭圆的标准方程问题，根据题设条件和椭圆的定义，即可求出椭圆的方程；

（Ⅱ）本题考察的是圆锥曲线中的最值与范围问题，由于直线方程的斜率存在与否未知，需要分直线斜率存在和不存在的两种情况讨论，再联立方程组，利用韦达定理和弦长公式，得到，再利用基本不等式即可求出所求答案。

试题解析：（1）因为直线的倾斜角为， ，所以，直线的方程为，

由已知得，所以．又，所以， ,

椭圆的方程．

（2）当直线的斜率不存在时， 两点关于轴对称，则，

由在椭圆上，则，而，则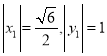

知=．

当直线的斜率存在时，设直线为，代入可得

，即，由题意，即．

．

， ,

化为， ，

即．

则，满足,

由前知， ，

．

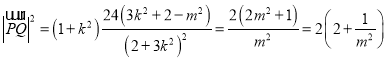
，当且仅当，即时等号成立，

故．

综上可知的最大值为．

[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2015/12/14/1572357219860480/1572357226373120/EXPLANATION/e9a188fc269d42bdb85c3fefe32573fd.png]