题目内容
（本小题满分14分）
设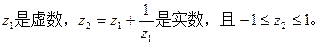
（1）求 | z1| 的值以及z1的实部的取值范围；
（2）若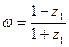
，求证：
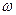为纯虚数。
解：(1)设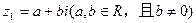
，则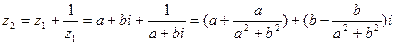
因为 z2是实数，b≠0，于是有a2+b2=1，即|z1|=1，还可得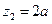
由-1≤z2≤1，得-1≤2a≤1，解得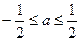
，即z1的实部的取值范围是
.
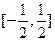（2）
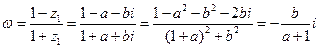
因为aÎ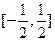，b≠0，所以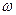为纯虚数.
解析
练习册系列答案
相关题目
题目内容
（本小题满分14分）
设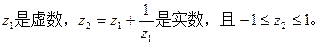
（1）求 | z1| 的值以及z1的实部的取值范围；
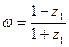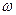（2）若，求证：为纯虚数。
解：(1)设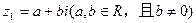，则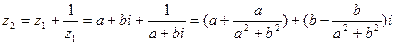
因为 z2是实数，b≠0，于是有a2+b2=1，即|z1|=1，还可得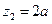
由-1≤z2≤1，得-1≤2a≤1，解得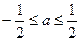，即z1的实部的取值范围是.
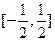（2）
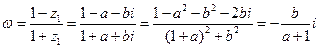
因为aÎ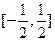，b≠0，所以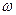为纯虚数.
解析
．
，复数
，
.
取何值时，
是实数；
.
．
及
；
，求实数
的值．
-(3-2i)
x-6i="0." (1)若x∈R,求x的值. (2)若x∈C,求x的值. 
在复平面内对应的点在第三象限。
的取值范围；
的最小值，并求出此时
满足
，则行列式
的最小值为 ．
，如果
，求实数
、
的值
，且
为纯虚数．
；
，求复数
的模
．