题目内容
13.已知空间向量$\overrightarrow{a}$=(x-1,1,-x),$\overrightarrow{b}$=(-x,3,-1),若$\overrightarrow{a}$⊥$\overrightarrow{b}$,则x的值为-1或3.分析 由$\overrightarrow{a}$⊥$\overrightarrow{b}$,可得$\overrightarrow{a}•\overrightarrow{b}$=0,解出即可.
解答 解:∵$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=-x(x-1)+3+x=0,
化为x2-2x-3=0,
解得x=3或-1.
故答案为:-1或3.
点评 本题考查了向量垂直与数量积之间的关系,考查了计算能力,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
18.圆x2+y2-2x+4y+3=0的圆心坐标为( )
| A. | (-2,4) | B. | (2,-4) | C. | (1,-2) | D. | (-1,2) |
5.若角α的终边落在直线y=3x上,则cosα的值为( )
| A. | ±$\frac{\sqrt{10}}{5}$ | B. | ±$\frac{\sqrt{10}}{10}$ | C. | ±$\frac{1}{3}$ | D. | ±$\frac{1}{5}$ |
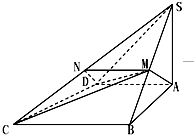 如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.
如图,四棱锥S-ABCD中,SA⊥底面ABCD,AB⊥AD,AD∥BC,SA=AB=BC=4,AD=2,M为SB的中点.