Question

【题目】设函数f（x）= ，若方程f（f（x））=a（a＞0）恰有两个不相等的实根x1 ， x2 ， 则e e 的最大值为（ ）
A.
B.2（ln2﹣1）
C.
D.ln2﹣1

Answer 1

【答案】C
【解析】解：令g（x）=f（f（x））= ， ∵y=f（x）在（﹣∞，0）上单调递减，在[0，+∞）上单调递增，
∴g（x）=f（f（x））在（﹣∞，0）上单调递减，在[0，+∞）上单调递增．
做出g（x）=f（f（x））的函数图象如图所示：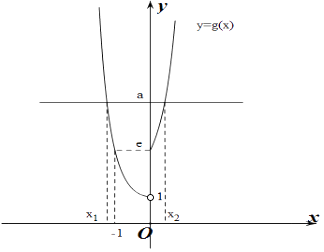

∵方程f（f（x））=a（a＞0）恰有两个不相等的实根x1 ， x2 ，
不妨设x1＜x2 ， 则x1≤﹣1，x2≥0，且f（x1）=f（x2），即x12=e ．
∴e e =e x12 ，
令h（x1）=e x12 ， 则h′（x1）=e （x12+2x1）=e x1（x1+2），
∴当x1＜﹣2时，h′（x1）＞0，当﹣2＜x1＜﹣1时，h′（x1）＜0，
∴h（x1）在（﹣∞，﹣2）上单调递增，在（﹣2，﹣1）上单调递减，
∴当x1=﹣2时，h（x1）取得最大值h（﹣2）= ．
故选C．
求出f（f（x））的解析式，根据f（f（x））的函数图象判断x1 ， x2的范围和两根的关系，构造函数h（x1）=e e ，求出h（x1）的最大值即可．