题目内容
10.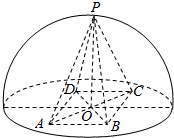 如图,四棱锥P-ABCD在半径为R的半球O内,底面ABCD是正方形,且在半球的底面内,P在半球面上,PO⊥平面ABCD,若VP-ABCD:V半球O=1:2π,则四棱柱P-ABCD的外接球的半径为R.
如图,四棱锥P-ABCD在半径为R的半球O内,底面ABCD是正方形,且在半球的底面内,P在半球面上,PO⊥平面ABCD,若VP-ABCD:V半球O=1:2π,则四棱柱P-ABCD的外接球的半径为R.
分析 设正方形ABCD的边长为a,PO=R,利用VP-ABCD:V半球O=1:2π,求出a=$\sqrt{2}$R,可得AO,即可求出四棱锥P-ABCD的外接球的半径.
解答 解:设正方形ABCD的边长为a,PO=R,则
∵VP-ABCD:V半球O=1:2π,
∴$\frac{1}{3}$•a2R:$\frac{4}{3}π{R}^{3}$=1:2π,
∴a=$\sqrt{2}$R,
∴AO=R,
∴四棱锥P-ABCD的外接球的半径为R,
故答案为:R.
点评 本题考查四棱锥、球的体积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知等差数列{an}的前n项和为Sn,若a2+a7+a12=24,则S13=( )
| A. | 18 | B. | 36 | C. | 54 | D. | 104 |