题目内容
5.已知圆C:(x-1)2+(y-2)2=25及直线l,且直线l过点(3,1).(1)证明:直线l与圆C恒相交;
(2)求直线l被圆C截得的弦长的最短长度及此时的直线方程.
分析 (1)利用两点间的距离公式求出AC之间的距离d,判断d小于半径5,得证;
(2)根据圆的对称性可得过点A最长的弦是直径,最短的弦是过A垂直于直径的弦,所以连接AC,过A作AC的垂线,此时的直线与圆C相交于B、D,弦BD为最短的弦,接下来求BD的长,根据垂径定理可得A是BD的中点,利用(1)圆心C到BD的距离其实就是|AC|的长和圆的半径|BC|的长,根据勾股定理可求出$\frac{1}{2}$|BD|的长,求得|BD|的长即为最短弦的长;根据点A和点C的坐标求出直线AC的斜率,然后根据两直线垂直时斜率乘积为-1求出直线BD的斜率,又直线BD过A(3,1),根据斜率与A点坐标即可写出直线l的方程.
解答 解:(1)直线l过点A(3,1).
又因为点A(3,1)与圆心C(1,2)的距离d=$\sqrt{5}$<5,
所以该点在C内,故不论m取什么实数,直线l与圆C恒相交.
(2)连接AC,当直线l是AC的垂线时,此时的直线l与圆C相交于B、D.BD为直线l被圆所截得的最短弦长.
此时,|AC|=$\sqrt{5}$,|BC|=5,所以|BD|=4$\sqrt{5}$.即最短弦长为4$\sqrt{5}$.
又直线AC的斜率kAC=-$\frac{1}{2}$,所以直线BD的斜率为2.
此时直线方程为:y-1=2(x-3),即2x-y-5=0.
点评 本题考查学生会求两直线的交点坐标,会利用点到圆心的距离与半径的大小比较来判断点与圆的位置关系,灵活运用圆的垂径定理解决实际问题,掌握两直线垂直时斜率的关系,会根据斜率与一点坐标写出直线的方程,是一道综合题.

练习册系列答案
相关题目
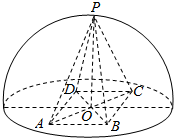 如图,四棱锥P-ABCD在半径为R的半球O内,底面ABCD是正方形,且在半球的底面内,P在半球面上,PO⊥平面ABCD,若VP-ABCD:V半球O=1:2π,则四棱柱P-ABCD的外接球的半径为R.
如图,四棱锥P-ABCD在半径为R的半球O内,底面ABCD是正方形,且在半球的底面内,P在半球面上,PO⊥平面ABCD,若VP-ABCD:V半球O=1:2π,则四棱柱P-ABCD的外接球的半径为R.