题目内容
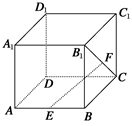
(本题满分12分) 如图,平面 ⊥平面
⊥平面 ,其中
,其中 为矩形,
为矩形, 为梯形,
为梯形,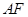 ∥
∥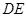 ,
,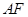 ⊥
⊥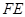 ,
,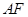 =
=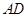 =2
=2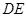 =2,
=2,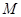 为
为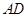 中点.
中点.
(Ⅰ) 证明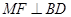 ;
;
(Ⅱ) 若二面角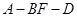 的平面角的余弦值为
的平面角的余弦值为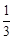 ,求
,求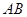 的长.
的长.
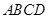 ⊥平面
⊥平面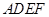 ,其中
,其中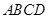 为矩形,
为矩形,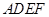 为梯形,
为梯形,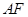 ∥
∥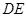 ,
,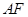 ⊥
⊥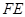 ,
,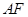 =
=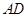 =2
=2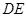 =2,
=2,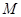 为
为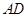 中点.
中点.(Ⅰ) 证明
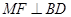 ;
;(Ⅱ) 若二面角
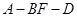 的平面角的余弦值为
的平面角的余弦值为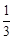 ,求
,求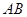 的长.
的长.
(Ⅰ) 证明见解析(Ⅱ)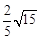
试题分析:(Ⅰ)由已知
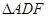 为正三角形,
为正三角形,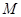 为
为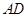 中点,所以
中点,所以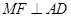 ,
,因为平面
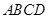 ⊥平面
⊥平面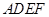 ,平面
,平面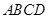
 ⊥平面
⊥平面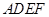
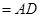 ,
,所以
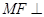 平面
平面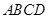 ,所以
,所以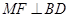 . ……4分
. ……4分(Ⅱ) 方法一:设
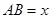 .取
.取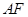 的中点
的中点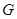 ,由题意得
,由题意得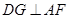 .
.因为平面
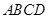 ⊥平面
⊥平面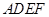 ,
,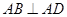 ,所以
,所以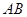 ⊥平面
⊥平面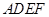 ,
,所以
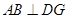 ,所以
,所以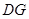 ⊥平面
⊥平面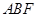 .
.过
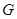 作
作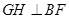 ,垂足为
,垂足为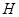 ,
,连结
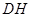 ,则
,则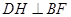 ,
,所以
 为二面角
为二面角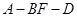 的平面角. ……8分
的平面角. ……8分在直角△
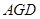 中,
中,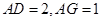 ,得
,得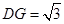 .
.在直角△
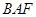 中,由
中,由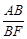 =sin∠AFB=
=sin∠AFB=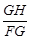 ,得
,得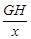 =
=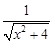 ,所以
,所以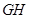 =
=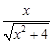 .
.在直角△
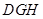 中,
中,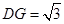 ,
,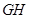 =
=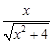 ,得
,得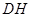 =
=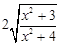 .
.因为
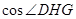 =
=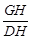 =
=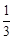 ,得x=
,得x=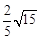 ,所以
,所以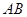 =
=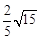 . ……12分
. ……12分方法二:设
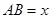 .以
.以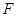 为原点,
为原点,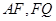 所在的直线分别为
所在的直线分别为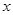 轴,
轴,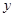 轴建立空间直角坐标系
轴建立空间直角坐标系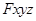 .
.则
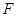 (0,0,0),
(0,0,0),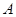 (-2,0,0),
(-2,0,0),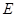 (
(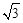 ,0,0),
,0,0),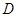 (-1,
(-1,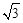 ,0),
,0),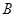 (-2,0,
(-2,0,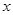 ),
),所以
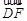 =(1,-
=(1,-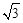 ,0),
,0),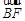 =(2,0,-
=(2,0,-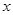 ).
).因为
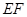 ⊥平面
⊥平面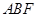 ,所以平面
,所以平面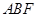 的法向量可取
的法向量可取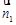 =(0,1,0).
=(0,1,0).设
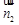 =
=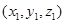 为平面
为平面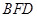 的法向量,则
的法向量,则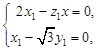
所以,可取
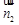 =(
=(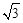 ,1,
,1,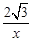 ).因为cos<
).因为cos<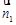 ,
,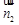 >=
>=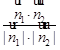 =
=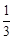 ,
,得x=
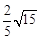 ,所以
,所以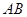 =
=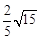 . ……12分
. ……12分点评:遇到立体几何的证明题,要紧扣定理,要把定理要求的条件一一列清楚;而利用空间向量解决立体几何问题时,要建立右手空间直角坐标系,要准确计算.

练习册系列答案
相关题目

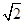
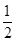
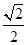
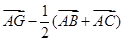 =
= β,给出四个命题:( )
β,给出四个命题:( )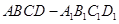 的底面边长为2,高为4,则异面直线
的底面边长为2,高为4,则异面直线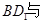
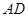 所成角的正切值是_________________.
所成角的正切值是_________________.
 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 ,且
,且 ,过
,过 ,则
,则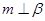
 所在的平面
所在的平面 和四边形
和四边形 所在的平面
所在的平面 互相垂直,且
互相垂直,且 ,
, ,
,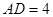 ,
, ,
, .若
.若 ,则动点
,则动点 在平面
在平面