题目内容
正方体ABCD—A1B1C1D1中,E、F分别是AB、B1C的中点,则EF与平面ABCD所成的角的正切值为( )
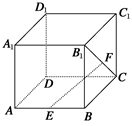
A. 2
B.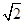
C.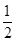
D.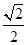

A. 2
B.
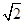
C.
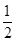
D.
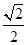
D
试题分析:设正方体的棱长为a,取BC得中点M,连接ME,MF,由正方体的性质可知MF⊥平面ABCD,则∠MEF即为直线EF与平面ABCD所成的角。在Rt△MEF中,∠FME=90°,FM=
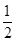 a,ME=
a,ME=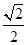 a,所以tan∠FEM=
a,所以tan∠FEM=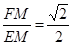 。故选D。
。故选D。点评:本题主要考查了直线与平面所成的角的求解,解题的关键是熟练利用正方体的性质要找到已知平面ABCD的垂线,然后在直角三角形中求解。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
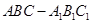 中,
中, 、
、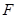 分别是
分别是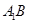 、
、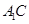 的中点,点
的中点,点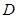 在
在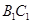 上,
上,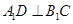 。
。
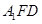
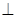 平面
平面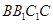
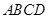 ⊥平面
⊥平面 ,其中
,其中 ∥
∥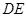 ,
,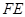 ,
,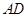 =2
=2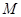 为
为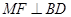 ;
;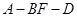 的平面角的余弦值为
的平面角的余弦值为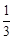 ,求
,求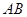 的长.
的长.
 、
、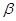 表示不同平面,下列命题正确的是 ( )
表示不同平面,下列命题正确的是 ( )

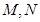 分别是
分别是 中点)
中点)
 平面
平面 ;
;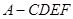 的体积.
的体积.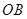 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为 ,
,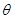 (rad),将y表示成
(rad),将y表示成
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: ,
, ,则
,则 ;②若
;②若 ,
, ,
, ,
, ,则
,则 ,则
,则 ; ④若
; ④若 ,
, ,
, ,
, ,则
,则 .其中真命题的个数是
.其中真命题的个数是