题目内容
已知直线l,m,平面α,β,且l⊥α,m β,给出四个命题:( )
β,给出四个命题:( )
①若α∥β,则l⊥m;②若l⊥m,则α∥β;③若α⊥β,则l∥m;
其中真命题的个数是( ).
 β,给出四个命题:( )
β,给出四个命题:( )①若α∥β,则l⊥m;②若l⊥m,则α∥β;③若α⊥β,则l∥m;
其中真命题的个数是( ).
| A.3 | B.2 | C.1 | D.0 |
C
试题分析:对于直线l,m,平面α,β,且l⊥α,m
 β,那么当
β,那么当① 若α∥β,则根据面面平行,可知l⊥β,则l⊥m;利用线垂直的性质定理得到结论,成立。
②若l⊥m,则α∥β;也可能面面是相交的时候,不成立,
③若α⊥β,则l∥m,两直线的情况还可能是相交,或者异面,因此不成立,选C.
点评:解决该试题的关键是理解诶线面垂直的性质定理,和线线平行的判定定理的运用,面面平行的判定定理的熟练运用。

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
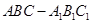 中,
中,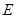 、
、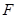 分别是
分别是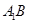 、
、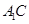 的中点,点
的中点,点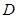 在
在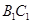 上,
上,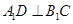 。
。
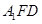
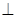 平面
平面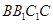
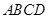 ⊥平面
⊥平面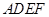 ,其中
,其中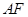 ∥
∥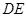 ,
,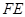 ,
,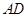 =2
=2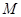 为
为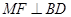 ;
;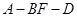 的平面角的余弦值为
的平面角的余弦值为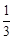 ,求
,求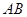 的长.
的长.
 中,
中,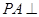 底面
底面 ,
, ,
, ,
,
 ,
, 是
是 的中点.
的中点. ;
; 平面
平面 ;
; 的正切值.
的正切值.
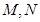 分别是
分别是 中点)
中点)
 平面
平面 ;
;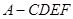 的体积.
的体积. 平面
平面 ,
,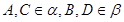 ,线段
,线段 与线段
与线段 交于点
交于点 ,若
,若 ,则
,则 = ( )
= ( )



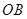 )为2m,在圆环上设置三个等分点A1,A2,A3。点C为
)为2m,在圆环上设置三个等分点A1,A2,A3。点C为 ,
,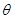 (rad),将y表示成
(rad),将y表示成
 为空间四边形
为空间四边形 的边
的边 上的点,且
上的点,且 ,求证:
,求证: