题目内容
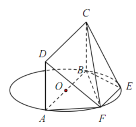
【题目】如图,AB为圆O的直径,点E、F在圆O上,AB![]() EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
EF,矩形ABCD所在平面和圆O所在平面垂直,已知AB=2,EF=1.
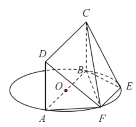
(I)求证:平面DAF⊥平面CBF;
(II)若BC=1,求四棱锥F-ABCD的体积.
【答案】(I)见解析;(II)![]() .
.
【解析】
(I)通过证明![]() ,证得
,证得![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .(II)矩形
.(II)矩形![]() 所在平面和圆
所在平面和圆![]() 所在平面垂直,点
所在平面垂直,点![]() 到边
到边![]() 的距离即为四棱锥FABCD的高,然后利用锥体体积公式求得四棱锥的体积.
的距离即为四棱锥FABCD的高,然后利用锥体体积公式求得四棱锥的体积.
(I)
∵AB为圆O的直径,点F在圆O上
∴AF⊥BF
又矩形ABCD所在平面和圆O所在平面垂直且它们的交线为AB,CB⊥AB
∴CB⊥圆O所在平面
∴AF⊥BC
又BC、 BF为平面CBF上两相交直线
∴AF⊥平面CBF
又![]()
∴平面DAF⊥平面CBF.
(II)连接OE
∵AB=2,EF=1,AB![]() EF
EF
∴OA=OE=1,即四边形OEFA为菱形
∴AF=OA=OF=1
∴等边三角形OAF中,点F到边OA的距离为![]()
又矩形ABCD所在平面和圆O所在平面垂直
∴点F到边OA的距离即为四棱锥F-ABCD的高
∴四棱锥F-ABCD的高![]()
又BC=1
∴矩形的ABCD的面积SABCD=![]()
∴![]()

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目