题目内容
【题目】将33![]() 33的方格表中毎个格染三种颜色之一,使得每种颜色的格的个数相等.若相邻两格的颜色不同,则称其公共边为“分隔边".试求分隔边条数的最小值。
33的方格表中毎个格染三种颜色之一,使得每种颜色的格的个数相等.若相邻两格的颜色不同,则称其公共边为“分隔边".试求分隔边条数的最小值。
【答案】56
【解析】
记分隔边的条数为L。首先,将方格表按图分成三个区域,分别染成三种颜色,粗线上均为分隔边。将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() 。行
。行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() 。三种颜色分别记为
。三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() 设
设![]() 为含有
为含有![]() 色方格的行数与列数之和。
色方格的行数与列数之和。
定义![]() 类似地定义
类似地定义![]() .计算得到
.计算得到![]()
![]() ,再证明
,再证明![]() ,再证明対任意
,再证明対任意![]() 均有
均有![]() 最后求出分隔边条数的最小值.
最后求出分隔边条数的最小值.
记分隔边的条数为L。首先,将方格表按图分成三个区域,分别染成三种颜色,粗线上均为分隔边。
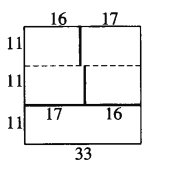
此时,共有56条分隔边,即L=56。
其次证明:L≥56。
将方格表的行从上至下依次记为![]() ,列从左至右依次记为
,列从左至右依次记为![]() 。行
。行![]() 中方格出现的颜色数记为
中方格出现的颜色数记为![]() ,列
,列![]() 中方格出现的颜色个数记为
中方格出现的颜色个数记为![]() 。三种颜色分别记为
。三种颜色分别记为![]() ,对于一种颜色
,对于一种颜色![]() 设
设![]() 为含有
为含有![]() 色方格的行数与列数之和。
色方格的行数与列数之和。
定义![]()
类似地定义![]() .
.
所以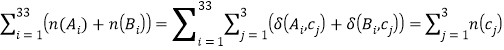
由于染![]() 色的格有
色的格有![]() 个,设含有
个,设含有![]() 色方格的行有a个、列有b个,则
色方格的行有a个、列有b个,则![]() 色的方格一定在这a行和b列的交叉方格中。
色的方格一定在这a行和b列的交叉方格中。
从而,![]()
所以![]() ①
①
由于在行![]() 中有
中有![]() 种颜色的方格,于是,至少有
种颜色的方格,于是,至少有![]() 条分隔边。
条分隔边。
类似地,在列![]() 中,至少有
中,至少有![]() 条分隔边。
条分隔边。
则![]() ②
②
![]() ③
③
下面分两种情形讨论。
1.有一行或一列所有方格同色。
不妨设有一行均为![]() 色则方格表的33列中均含有
色则方格表的33列中均含有![]() 色的方格,又
色的方格,又![]() 色方格有363个,故至少有11行含有
色方格有363个,故至少有11行含有![]() 色方格.于是,
色方格.于是,![]() ④
④
由式①、③、④得
![]()
(2)没有一行也没有一列的所有方格同色.
则対任意![]() 均有
均有
从而,由式②知;
![]()
综上,分割边条数的最小值为56.

 阅读快车系列答案
阅读快车系列答案【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
【题目】某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() 与该小卖部的这种饮料销量
与该小卖部的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)根据(1)中所得的线性回归方程,若天气预报1月16日的白天平均气温![]() ,请预测该奶茶店这种饮料的销量.
,请预测该奶茶店这种饮料的销量.
(参考公式: ,
,![]() )
)