题目内容
函数f(x)= 其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=
其中P,M为实数集R的两个非空子集,又规定f(P)={y|y=f(x),x∈P},f(M)={y|y=f(x),x∈M}.给出下列四个判断:①若P∩M=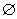 ,则f(P)∩f(M)=
,则f(P)∩f(M)=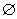 ; ②若P∩M≠
; ②若P∩M≠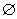 ,则f(P)∩f(M) ≠
,则f(P)∩f(M) ≠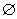 ;③若P∪M=R,则f(P)∪f(M)=R; ④若P∪M≠R,则f(P) ∪f(M)≠R其中正确判断的有( )
;③若P∪M=R,则f(P)∪f(M)=R; ④若P∪M≠R,则f(P) ∪f(M)≠R其中正确判断的有( )
| A.0个 | B.1个 | C.2个 | D.4个 |
C
解析试题分析:①举个反例 P="(0,1]" M=[-1,0] 显然f(-1)=f(1), ①错; ③若P∪M=R,则f(P)∪f(M)=R 举个反例 P=[0,+ ),M=[-
),M=[- ,0), ③错,∴正确的只有②④,故选C
,0), ③错,∴正确的只有②④,故选C
考点:本题考查了函数的性质
点评:掌握分段函数的定义域和值域是解决此类问题的关键

练习册系列答案
相关题目
若函数 的零点与
的零点与 的零点之差的绝对值不超过
的零点之差的绝对值不超过 ,则
,则 可以是
可以是
A. | B. |
C. | D. |
已知 ,关于
,关于 的方程
的方程 有相异实根的个数情况是( )
有相异实根的个数情况是( )
| A.0或1或2或3 | B.0或1或2或4 |
| C.0或2或3或4 | D.0或1或2或3或4 |
定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有
<0,则( )
| A.f(3)<f(-2)<f(1) | B.f(1)<f(-2)<f(3) |
| C.f(-2)<f(1)<f(3) | D.f(3)<f(1)<f(-2) |
已知函数 对任意
对任意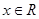 都有
都有 ,若
,若 的图象关于直线
的图象关于直线 对称,且
对称,且 ,则
,则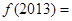
| A.2 | B.3 | C.4 | D.0 |
函数 的单调递减区间是( )
的单调递减区间是( )
A. | B. | C. | D. |

 与
与 (
( 且
且 )的图象可能是( )
)的图象可能是( )




 满足:
满足: 轴对称,并且对任意的
轴对称,并且对任意的
 有
有 ,则当
,则当 时,有( )
时,有( )


